Wilhelm Schickard

Wilhelm Schickard (see biography of Schickard) was born in the small south German town Herrenberg (near Tübingen) and educated in the Protestant theological seminary Tübinger Stift in Tübingen. He received his bachelor’s degree in 1609 and master’s degree in theology in 1611. In 1613 he became a Lutheran minister, continuing his work with the church until 1619, when he was appointed professor of Hebrew at the University of Tübingen, and in 1631 he became a professor of astronomy, mathematics, and geodesy.

Undoubtedly one of the most important events in the life of the modest deacon was his meeting in October, 1617, with the great astronomer Johann (Johannes) Kepler. Kepler, just like Schickard, had studied theology at Tübinger Stift (Kepler lived in Tübingen from 1589 till 1594) and worked as a Lutheran minister some 20 years before him, before devoting his life to mathematics and astronomy. Kepler visited Tübingen during one of his journeys in Württemberg, to see his old friend Michael Maestlin (1550-1631) (a famous German astronomer and mathematician, who used to be a mentor of Johann Kepler, and just like Schickard and Kepler, was Magister of theology at Tübinger Stift from 1571 and worked some time as a Lutheran deacon) and others.

It seems Schickard was recommended to Kepler just by Maestlin, who was Schickard’s teacher and precursor in the chair of astronomy. Maestlin probably was some kind of a patron for Schickard also (as he used to be for Kepler), because at that time there was no academic appointment without patronage.

Kepler wrote his first impressions of Schickard in his diary—”In Nürtingen I met also an excellent talent, a math-loving young man, Wilhelm, a very industrious mechanic and lover of oriental languages.” Obviously during this meeting Kepler immediately recognized the massive intellect of the young Wilhelm, and encouraged his occasions with sciences.

From this moment on, Schickard entered into close friendship and busy correspondence with Kepler until his death. During their acquaintance, Schickard made scientific investigations for Kepler, took care of Kepler’s son Ludwig (who was a student in Tübingen), created figures and copperplates by Kepler’s request, helped for the printing of Kepler’s renowned books, and (which is most interesting for us) designed a mechanical calculating machine. Schickard referred to the machine as Rechen Uhr—calculating meter or calculating clock, which proved to be the first mechanical calculating device ever created.

Kepler was a great admirer of the logarithms of Napier. When in 1617 he first saw a copy of Napier’s book on logarithms, he didn’t fully understand them. He wrote to Wilhelm Schickard saying that some Scottish nobleman had come up with a way of turning all multiplications and divisions into additions and subtractions, but later remarked that he doubted it would work properly. About a year later he reconsidered the concept and became so enthusiastic that he wrote to Napier (unfortunately he was already dead).

Unfortunately, the machine, designed by Schickard around 1623, didn’t manage to survive to the present day. Only 3 documents about this machine have been found until now—two letters from Schickard to Kepler, and a sketch of the machine with instructions to the mechanician.

The two letters have been discovered by a famous biographer of Kepler—Max Caspar, who worked in 1935 in the archive of Kepler, kept in the Pulkovo Observatory near S. Peterburg, Russia (Kepler’s manuscripts were bought by order of the Empress of Russia Екатерина II Великая (Catherine the Great) in 1774). While searching through a copy of Kepler’s Rudolphine Tables, Caspar found a slip of paper, that had seemingly been used as a bookmark. It was this slip of paper that contained Schickard’s original drawings of the machine (from the second letter to Kepler). Later Max Caspar stumbled upon the other pages of the two letters.
In the 1950s another biographer of Kepler—Dr. Franz Hammer (1898-1969), made a connection between the two letters from Pulkovo and a sketch of a machine (along with instructions to the mechanician—probably to Johann Pfister) described in Schickard’s manuscripts (Schickard sketchbook), kept in Württembergischen Landesbibliothek in Stuttgart (see the figures bellow).

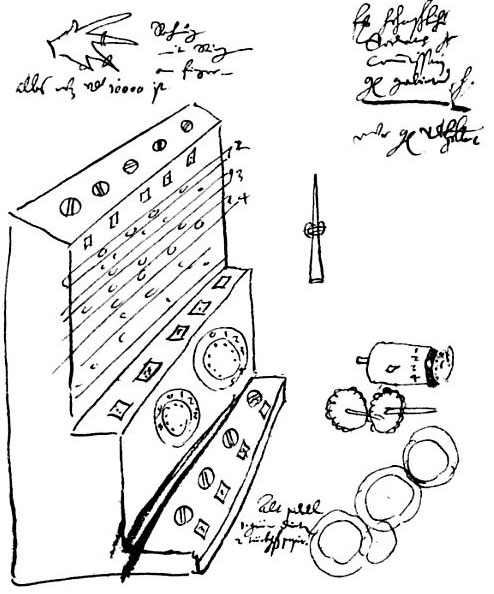
Caspar and Hammer however were not the first men, who noticed the machine of Schickard. Who was the first?

In 1718 one of the first biographers of Kepler—the German Michael Gottlieb Hansch (1683-1749), published a book of letters of Kepler, which includes the two letters from Schickard to Kepler. There is even a marginal note of the publisher Schickardi machina arithmetica at the second letter, obviously on the calculating machine.

In 1787, in the book “An account of the life, writings, and inventions of John Napier, of Merchiston”, the author—David Erskine, Earl of Buchan, mentioned that …Shickartus in a letter to Kepler, written in the year 1623, informs him that he had lately constructed a machine consisting of eleven entire and six mutilated little wheels, by which he performed the four arithmetical operations.
In 1899 in the Stuttgart’s surveying magazine Stuttgarter Zeitschrift für Vermessungswesen was published an old article for the topography in Württemberg, Germany, written many years ago and probably published in other editions, by the famous German scientist Johann Gottlieb Friedrich von Bohnenberger (1765–1831). In this article the name of Schickard is mentioned several times, not only concerning his important contribution in the field of topography, but it is mentioned also that …it is strange, that nobody admitted, that Schickard invented a calculating machine. In 1624 he ordered a copy for Kepler, but it was destroyed in a night fire. Bohnenberger (known mainly as the inventor of the gyroscope effect), just like Schickard, studied and later was appointed a professor of mathematics and astronomy at the University of Tübingen since 1798.

In 1912 in the yearly German magazine Nachrichten des Württembergischen Vermessungstechnischen Vereins was published the sketch and the notes of the machine from the Württembergischen Landesbibliothek. The author of the article A. Georgi was however probably not aware of the two letters of Schickard, but only with the note of Bohnenberger. He even claimed, that Leibnitz was aware of the machine of Schickard and accused him of plagiarism, which is unbelievable.

In April 1957, Hammer announced his discovery during the conference about the history of mathematics in Oberwolfach, Germany. From this moment on, gradually it was made known to the general public, that namely Schickard, but not Blaise Pascal, is the inventor of the first mechanical calculating machine.

In 1960 Mr. Bruno v. Freytag Löringhoff, professor of philosophy at the University of Tübingen, created the first replica of the Schickard’s machine.

The first letter—Wilhelm Schickard to Kepler in Linz, 20. September, 1623, includes (letters are written in Latin language, which was the international language of science and scholarship in Central and Western Europe until the 17th century):

…Porro quod tu logistice, idem ego mechanice nuper tentavi, et machinam extruxi, undecim integris et sex mutilatis rotulis constantem, quae datos numeros statim άώτομάτος computet, addat, subtrahat, multiplicet, dividatque. Rideres clare, si praesens cerneres, quomodo sinistros denarium, vel centenarium supergressos, sua sponte coacervet, aut inter subtrahendum ab eis aliquid suffuretur…

In English it sounds like—I have tried to discover a mechanical way for performing calculations, which you have done manually till now. I constructed a machine, which includes eleven full and six partial pinion wheels, which can calculate automatically, to add, subtract, multiply and divide. You would rest satisfied if you can see how the machine accumulates and shifts to the left tens and hundreds, and makes the opposite shift during a subtraction…

From 1612 to 1626, Kepler lived in Linz, Austria, where he worked as a mathematics teacher and as an astrologer. In this period (1623), he was completing his famous Tabulae Rudolphinae and certainly needed such a calculating instrument. He must have written back asking for a copy of the machine for himself, because the second letter, dated February 25th, 1624, includes a description of the machine with two drawings and bad news about a fire, which destroyed the machine:

…Arithmeticum organum alias delineabo accuratius, nunc et festinate hoc habe, aaa sunt capitella cylindrorum erectorum, quibus multiplicationes digitorum inscriptae, et prominent, quantum ijs opus est, per fenestellas bbb ductiles, ddd intus habent affixas rotulas 10 dentium, sic contextas, vt mota qualibet dextra decies, proxima sinistra semel; aut illâ 100 vicibus circumactâ, tertia semel etc. promoveatur. Et quidem in eandem partem; quod vt praestarem, intermediâ consimilj opus fuit. (A marginal note) Quaelibet intermedia omnes sinistras movet, debitâ proportione; nullam verò dextram, quod singularj cauitione indiguit. (End of the note) Quotus eorum prominet per foramina ccc in scamno medio, tandem in pavimento inferiorj e vertebras et similiter foramina pro apparitione numerorum notat, quibus inter operandum usus est. Sed ista sic tumultuariè scribj nequeunt, facilius ex autopsiâ cognoscentur. Et curaveram tibj jam exemplar confierj apud Joh. Pfisterum nostratem, sed illud semiperfectum, vna cum alijs quibusdam meis, praecipuè aliquot tabellis aeneis conflagravit ante triduum, in incendio noctu et ex improsivo ibj coorto, quod Mütschlinus referre amplius sciet. Harum jacturam admodum aegre fero, praesertum nunc quando non vacat alia reficere tam cito.

In English—…I will describe the computer more precisely some other time, now I don’t have enough time: aaa are the upper faces of vertical cylinders (see the upper figure), whose side surfaces are inscribed with multiplication tables. The digits of these tables can be looked out of the windows bbb of a sliding plate. From the inner side of the machine to the disks ddd are attached wheels with 10 cogs, and each wheel is clutched with a similar wheel in a manner that, provided some of the right wheels spins round ten revolutions, the left wheel will make one revolution, or provided the first wheel spins round 100 revolutions, the third wheel to the left will make one revolution. In order the revolutions of the wheels to be in the same direction, intermediate wheels are necessary. [See the following sketch]. [A marginal note] Each intermediate wheel moves to the left needed carry, but not to the right, which made special caution measures necessary. [End of the note].

The digits, inscribed upon each wheel, can be looked out of the windows ccc of the middle bank. In the end of the lower bank are arranged rotating heads eee, used for recording of numbers, which are the result of the calculations, and their digits can be looked out of the windows fff. I have already ordered a copy for you to our Johann Pfister, together with some other things for me, especially some copper plates, but when the work was half finished, yesterday night a fire burst out and everything burnt out, as Maestlin informed you. I take this loss very heavily, because there is no time for its replacement.

Schickard obviously was not satisfied with the work of the mechanician, involved in the production of the device, because the note to him begins (old German language is used):
Rechen Uhr betreffs.
1. Die zän seind gar vngleich und vnfleißig…
(which means in English, kindly translated by Mr Stephan Weiss, www.mechrech.info):
Concerning Calculating Clock,
1. The teeth are inequally made and don’t work…

That’s the whole information, survived up to the present for the Calculating Clock of Schickard. It seems the prototype of the machine, mentioned in the first letter, was rather successful, that’s why Schickard ordered the next copy for Kepler. It is unknown whether another copy was ever created, and how many devices are made or ordered by the inventor. It is out of the question however, that such device has not been delivered to Kepler. Most probably, only two machines were produced, the prototype, mentioned in the first letter, which was in the home of Schickard, and disappeared after his death, and second, made for Kepler, which was destroyed during the fire.

Not a whole lot is known of the mentioned in the second letter Joh. (Johannes) Pfister, who was involved not only in the production of Schickard’s calculating machines, but also in other projects such as preparing metal plates for his and Kepler’s books.

The Pfisters is a well-known for the time Tübinger family, known primarily as book-binders and Universitätspedells at the University of Tübingen (Universitätspedell was a relatively prominent position, responsible for arresting and detaining students in the karzer and functioning as prosecutor at the university court).

First was Hans Pfister, the Older (1523-1607), the grandfather of Johannes Pfister, who was not only a member of Tübinger’s book-binders guild, but also served a long time in University of Tübingen as a watch and Universitätspedell.

Hans Pfister’s son—Hans (Conrad) Pfister, Jr. (b. 1560) succeeded his father and worked as a book-binder, seal-engraver, Universitätspedell, and schoolmaster in Tübingen. He married Anna Ruckaberle in 1578 (1563-1624). The family had ten children, one of whom was Johannes Pfister.

Johannes Pfister was born on January 15, 1582, in Tübingen. He succeeded in the family trade and worked as a bookbinder and printer, as well as an engraver and mechanician. He must have also been a decent painter, because an interesting painting from 1620 survived to our time (see the upper painting of Pfister). Johannes married in 1606 to Rosina Steininger, a daughter of the Lutheran scholar Gall Steininger.

Let’s examine the structure and the functioning of the device, designed by Schickard and produced by Pfister. The Calculating Clock is composed of 3 main parts:

• A multiplying device.
• A mechanism for recording of intermediate results.
• A decimal 6-digit adding device.

The multiplying device is composed of 6 vertical cylinders with inscribed numbers of Napier’s rods (see the photo below).

From the front side, the cylinders are covered with 9 narrow plates with windows, which can be moved leftwards and rightwards. After entering of the multiplicand by rotating the cylinders through the knobs in the upper side of the box, by means of opening of the windows of plates can be made consecutive multiplying first by units of the multiplier, then by tens, and so on. The intermediate products can be added by means of adding device.

The mechanism for recording of intermediate results of calculations is composed of 6 rotating through small knobs disks with peripheries inscribed with digits, which can be seen in the small windows in the lower row (see the photo below). These disks are not connected with the calculating mechanism and don’t have a tens carry mechanism.

The adding device is composed of six basic axes in a row. On each axis is mounted a smooth disk with ten openings (marked with 1 in the lower photo), a cylinder with inscribed digits (marked with 3), and a pinion wheel with 10 teeth (marked with 2), over which is fixed pinion wheel with 1 tooth (which are used for tens carry). On the other 5 axes are mounted pinion wheels with 10 teeth (marked with 4).

The smooth disks are used for entering the numbers and resetting the machine. The digits on the inscribed cylinders can be seen in the upper row of windows and are used for reading the results of adding and subtracting operations. Over each of the 10-teeth disks on the basic axes is mounted a one-tooth disk, in such manner, that for each full revolution of 10-teeth disk, 1-tooth disk enters once in a contact with the according intermediate disk and rotates it to 1/10 revolution. This is the mechanism of tens carry and it is not original. The use of an analog train of gear wheels (linked so that each time one wheel completes a revolution the next wheel turns one-tenth of a revolution, thus recording a carry) is very ancient and even appears in the works of Heron of Alexandria

The axes can be rotated in both directions, so the machine can be used not only for addition, but for direct subtraction too (no need to use the arithmetical operation complement to 9, as it was the case with Pascaline). Due to the intermediate disks, all smooth disks are rotated in the same direction.

The machine has also an indicator for overflow—a small bell, which rings if the leftmost pinion wheel rotates from 9 to 0.

Let’s make a simple multiplication with the machine, for example 524×48. First we have to rotate the rightmost cylinder to 4, next cylinder to 2, and the third from right to 5 (the multiplicand is 524). Then we have to open the windows on the 8th row (units of the multiplier are 8) and we will see in the windows the first intermediate result (4192). We have to enter the 4192 in the calculating mechanism. Then we have to open the windows on the 4th (tens of multiplier are 4) row and to see the second intermediate result—20960, which we have to enter to the calculating mechanism, and we will have the result—25152.

As described by Schickard, the mechanism presented two eventual faults. First, the inventor didn’t describe a means for fixing the intermediate disks, which is certainly necessary. As you can see in the photos, the technicians of Mr. Freytag Löringhoff have provided such a mechanism (the small disks below the intermediate disks). The second problem is the friction. At the beginning of the 17th century, the turret lathes had not been invented yet, so the pinion wheels have to be produced manually and with great precision, otherwise the friction in case of full carrying (for example when to 999999 must be added 1) will be enormous and the machine will be hard to operate and easily broken. Schickard obviously had faced such problems, and that’s why his machine has only six main axes, in spite of the vital necessity of Kepler to work with big numbers for his astronomical calculations.

Up Next…

John Napier – Napier was a nobleman credited with coining the term logarithm.

Wilhelm Schickard – Learn the full biography and history of Schickard.

The History of People Behind Modern Computing – Discover the full history of computing and the many people who were involved in its evolution.

The image featured at the top of this post is ©G-Stock Studio/Shutterstock.com.