History of Computers and Computing, Mechanical calculators, 19th century, Maurel and Jayet
The arithmaurel of Maurel and Jayet
In 1841 in Paris the young French student François Timoléon Maurel (later a good French clockmaker) devised and in the next 1842 patented (patent No. FR14529) his first calculating machine for multiplication and division, which certainly can be used for addition and subtraction also.
In 1846 Maurel patented (this time together with his older friend—the engineer Jean Jayet (1796-1856,) an improved version of the machine (see the patent FR4777). The prototype of the device was presented at the Exposition nationale de 1849 à Paris and caused a sensation, being awarded the gold medal. Subsequently, the machine was awarded the Prix de mécanique of the Fondation Montyon. Maurel was the holder of another French patent from 1860 for a calculating machine (No. 46757), as well as several patents in other countries, e.g. Austria and England.

The Arithmaurel of Maurel and Jayet from 1854 (© Musée des arts et métiers, Paris)
The machine became famous under the name Arithmaurel

Encouraged by the early success of the machine, the inventors planned to start mass production of their device, and assigned the production to the famous Austrian-French clockmaker Joseph-Thaddäus Winnerl (1799-1886), one of the best watchmakers in Europe. Winnerl (see the nearby image), was born in Mureck, Styria, and was trained and worked in Austria, Germany, and Denmark, but in 1829 he settled in France, where in 1831 he established his own workshop in Paris and soon became an outstanding manufacturer of chronometers, marine clocks, and balance wheels.
Until 1854, Winnerl was not able to build any of the 8-digit machines (a minimum for any professional usage) that had been ordered, but until the late 1850s about thirty handmade copies of Arithmaurel were produced in his workshop, and several devices managed to survive to our time. Unfortunately, the construction of the machine was too complex for the technology of the middle of the 19th century. The devices were expensive, fragile, and error-prone, so they were not competitive with the simpler, but cheap and reliable calculating machines of Colmar
The dimensions of the machine are 20,5 x 18,2 x 29 cm. Materials used are bronze, enamel plates, and mahogany (for the body).
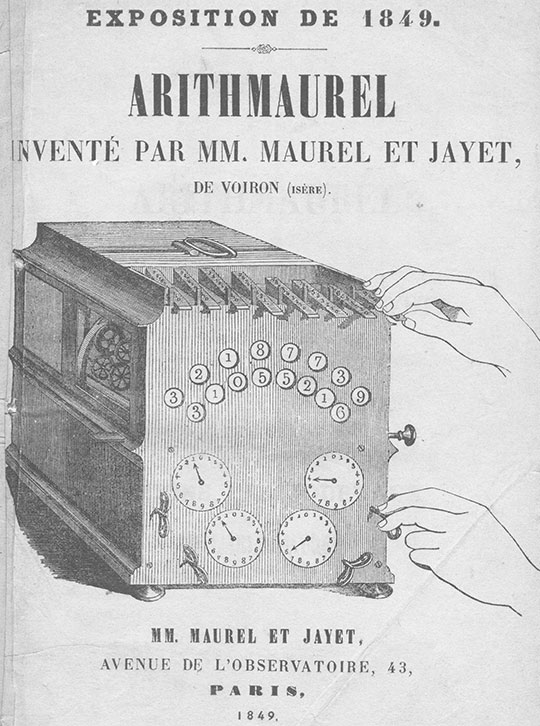
The Arithmaurel of Maurel and Jayet
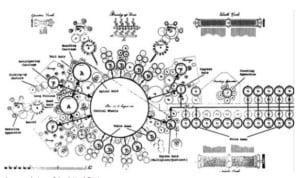
The calculating mechanism is based on the stepped drum of Leibniz. The multiplicand is entered by means of the stems in the upper part of the machine. Pulling or pushing these stems, the stepped drums in the box will be moved, so different numbers of teeth will be contacted by the calculating mechanism during the rotation of the handle. The multiplier is entered by means of the four keys in the lower part of the machine and can be seen in the four dials near the keys. On the dials are inscribed two rows of digits (from 0 to 9) on the left and right parts of the dial. The first half is used during the division, while the other part is used during the multiplication. After entering of the multiplicand and multiplier, by rotating the handle on the right side of the box, the calculating mechanism and drums will make one revolution and the result can be seen in the central dials. The upper row of dials is for storing of the intermediate result during the multiplication of more than two numbers.
During the division, the keys must be rotated in the direction, contrariwise to the multiplication. The reset mechanism is placed on the side.
The described in the patent machine can be used for the multiplication of 8-digit to 4-digit numbers, the result mechanism is also 8-digit. There are also machines with a different number of positions.

According to a book from 1853, using the Arithmaurel a multiplication of two 8-digit numbers can be done for 18 seconds, while the division of 15-digit to 8-digit numbers can be done for 24 seconds, which was a remarkable calculating speed at that time.
The image featured at the top of this post is ©G-Stock Studio/Shutterstock.com.