Ramón Verea

Ramón Verea

In 1878 Ramón Silvestre Verea García (1833-1899), a Spaniard, and newspaper publisher in New York, patented a direct-multiplying machine, which proved to be the second patented machine of this type (after the machine of Edmund Barbour), 10 years before the first popular direct-multiplying machine of León Bollée

Most early calculating machines carried out multiplication as a form of repeated addition. To multiply, say, by sixteen, one set the carriage at its rightmost position, turned the operating crank six times, shifted the carriage one position to the left, and turned the crank once. In direct-multiplying calculating machines, the operator had only to perform operations when the multiplier was a digit number.

Ramón Verea (see biography of Ramón Verea) was a very interesting person. Born in 1833 in Galicia, Spain, he lived for 10 years in Cuba and in 1865 settled in New York, working as a journalist in a magazine, agent for inventions, and trading with Spanish gold and banknotes, which got him interested in calculation.

The inventor himself listed in an article in the New York newspaper Las Novedades, issue 1 April 1881, his motives to create the calculating machine:

My object in undertaking an invention at first sight impossible it was not the hope of refunding even a part of several thousand dollars that I have spent; neither it was to became a celebrity like others, my ambition was driven by:

1) A little egoism;
2) Much patriotism, the desire to prove that in inventive genius a Spaniard can leave behind the eminences of the most cultured nations;
3) The innate eagerness to contribute something to the advancement of science; and lastly
4) Entertainment according to my tastes and inclinations.

On 5 July 1878, Verea applied, and on 10 September 1878, he received a U.S. patent №207918 for his machine. It seems, he manufactured also two prototypes, one of them sent together with the patent application to the US Patent Office, and the second, which the same year (1878) was exposed and won a gold medal of the Exposición Mundial de Inventos de Cuba in Matanzas, Cuba.

The advanced calculating machine of Verea didn’t remain unnoticed. Soon many newspapers like New York Herald, Scientific American, Le Courrier, Las Novedades, published articles about the machine. In the Scientific American, Vol. 39, Nr. 16 of October 1878, the message was short: Mr. Ramon Verea, of New York City, has patented an improved Calculating Machine. This ingenious machine is capable of rapidly performing addition, subtraction, multiplication, and division. The details of its construction cannot be properly described without engravings

In the New York Herald article (later reprinted in other newspapers, like Morning Journal and Courier, New Haven, Conn., April 13, 1881) the machine of Verea was described in more detail (see below):

Multiplication by Machinery.

A Lot of Cogs and Wheels that Perform Arithmetical Calculations with Wondrous Rapidity and Accuracy.

Nothing seems more paradoxical than to perform the arithmetical operations, which appear to belong exclusively to the mind, by a combination of metallic pieces. Pope Sylvester II, to whom the world is indebted for the system of Arabic figures, tried to make a calculating machine.
Pascal and Leibnits spent years in vain attempts to solve the problem of mechanical mathematical calculation, and others worked at the same task until Thomas de Colmar, the French mathematician, discovered a method in 1822. Elaborations of the principles contained in his machine have been numerous but all results have only succeeded in perfecting a way to add and subtract. This made multiplication possible by adding one factor to itself as many times as there were units in the other factor, but the process was long and tedious.

Mr. Ramon Verea, a Spanish resident of New York, has been devoting his leisure hours for several years in developing a machine that will multiply and divide, and has finally succeeded. It will produce a product having fifteen figures and the factors may be of nine or less than nine and six or less than six figures. A turn of a small crank once for each figure in the multiplier displays the product on a disc. The work is almost instantaneous and the accuracy of it unimpeachable.
The machine consists of ten circular plates placed vertically, and on the edge of each are figures from 1 to 9 inclusive and zero. On the sides of these plates are points which form in substance a multiplication table. Suppose 9 is to be multiplied by 6. The first plate is turned so that nine shows on top; the other factor is then shown on a wheel belonging to a similar set as those on, which nine is shown. When the crank is turned the multiplicand plate turns six-ninths of a revolution and a point on the fourth concentric circle of points on the side of the plate is presented on one side and a point on the fifth concentric circle on the other.
These two points meet each a small tongue which operates upon the product box, where the result is directly shown. The mechanism by which the product is recorded is too complicated to admit of a description except at great length. There are a series of wheels worked upon, each of them graduated as to size and shape with the concentric circles on the plates. It might be said that in the multiplication the additions necessary are made simultaneously with the multiplication.
For example, multiplying 56 by 7 the process is 7 times 6 are 42, 7 times 5 are 35 and 4 are 39-product, 392. With the machine the work is instantaneous. When the wheel is turned the record is first made of 42 and then of 35, that is the 5 is at once added to the figure in the place of the tens of the other number, and the entire product “bobs up serenely” as the crank completes the revolution. If the multiplier were a double number, say 56 by 27, another turn of the crank would make the multiplication and addition complete. To prove the operation, pressing a button throws into gear a new set of wheels, and a turn of the crank reduces all the numbers in the product box to zero. Should zero not at once appear it would prove the original operation was wrong.

Mr. Verea explains that he did not make the machine either to sell its patent or to put it into use, but simply to show that it was possible and that a Spaniard can invent as well as an American. A number of the tests that were made in the presence of a Herald reporter and other visitors were conducted with facility and accuracy. The operation of multiplying 9,000,000 by 9,000 was correctly performed by the machine while the reporter and an accountant were trying to write out the product which they had already arrived at by a mental process.

Sadly, soon the sands closed over the machine of Verea (just like that of his predecessor Edmund Barbour). He never tried to market it. He just walked away and never invented anything else. As he said: “I just moved the desire to contribute something to the advancement of science and a little self-esteem. I am a journalist and not a scientist and also what I wanted to show… is already proven.”

The prototype of the Verea’s machine, sent to the Patent Office

The prototype of Verea’s machine, which was sent by the inventor to the US Patent Office, together with the application in July, 1878, was kept in the tanks of the headquarters of IBM in White Plains (New York) to be part of the collection begun in 1930 by the founder of IBM—Thomas Watson.

Verea’s calculator was a made of iron, brass and steel machine about 25 kilograms, 35 cm long, 23 cm wide and 20 cm high. It was able to add, multiply and divide numbers of nine figures, allowing up to six numbers in the multiplier and fifteen in the product. The multiplication solved through the direct method, based on a mechanism patented by Edmund D. Barbour in 1872. Verea saw how to do the whole multiplication in one stroke of a lever.

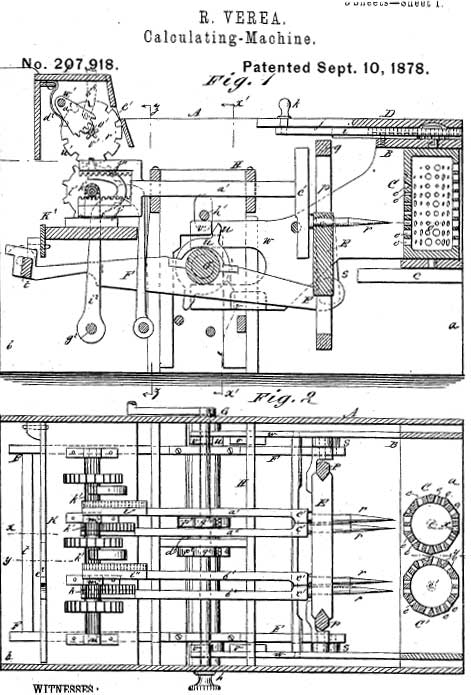
One of the patent drawings of the Verea’s machine

The basis of his machine was a ten-sided metal prism or cylinder (at the front side of the device you can see the two ten-sided brass cylinders, that are mounted vertically). Each of the sides of the each cylinder has two columns of holes, with ten holes in a column. The holes come in ten sizes, with the largest and deepest representing zero, and the smallest and shallowest, 9. The holes represent multiples of a given digit.

Above the cylinders are two knobs that move in slots in the flat top of the machine. Pulling forward a knob rotates the cylinder below, so that the side facing the back of the machine has holes representing multiples of the digit desired. Behind this mechanism is a row of tapered pins. Pulling a lever at the back of the machine raises or lowers these pins in order to set the multiplier. Turning a crank on the right side moves the pins up to the faces of the cylinders and, where there are holes in the cylinder, allows the pins to enter to a certain depth.

Once the surface of a cylinder touched a pin, it pushed the pin, and a rack behind the pin, backward. Pins entering shallow holes reach the cylinder quickly and have a correspondingly greater effect on the rack. Pinions linked to the racks rotate correspondingly, rotating the result wheels at the back of the machine, with carrying occurring as required. Further turning of the crank restores the cylinder, racks, and pins to their original position.

Ramon Verea’s calculating machine

It seems the prototypes of the machine, although looking primitive, worked perfectly for demonstration purposes. During one of the demonstrations (different from the previously mentioned demo in the presence of New York Herald reporter), the device could multiply 698543721 x 807689 in twenty seconds, an amazing speed for the time.

Next Up…

• James White
• Emory Seymour Ensign
• Gauss of Christel Hamann

The image featured at the top of this post is ©Public domain, via Wikimedia Commons.