
Michael Bouchet
Michael Bouchet (1827-1903) from Louisville, Kentucky, USA, was a holder of two USA patents for single-column adding devices (known also as single digit adders)—Patent №251823 from 1882 (assigned 1/2 to Bennett Downs Mattingly, a local distiller) and Patent №314561 from 1885.
Monsignor Michael Bouchet was a Frenchman, born on the farm of his parents Michael and Jeanne Saby-Bouchet in Le Milliazeix, Miremont, Auvergne, on 23 August 1827. Bouchet immigrated to the USA in May 1853, studied, and served in several places until 1860, when he settled in Louisville, Kentucky, to serve the local Catholic community.
Here he became not only a renowned pastor but also a linguist and inventor. Bouchet was Vicar General of the Archdiocese of Louisville from 1871 until his death on 12 April 1903, and rector of the Catholic Cathedral of the Assumption.
Michael Bouchet was a small, lively man, with an inventive turn of mind, devising automatic snakes to frighten his acolytes, and a folding bed and fire escape for his own use. He had considerable responsibility for the financial affairs of his diocese and, according to his biographer, as early as the 1860s devised an adding machine to assist in keeping these accounts. Of these devices, Bouchet patented only later versions of the adding machine, taking out the above-mentioned patents №251823 and №314561.
The second calculating device of Michael Bouchet was in fact an improved version of the first. Later on Bouchet deeded 1/3 of the rights of his second Patent №314561 to M. F. Madden, owner of the company M. F. Madden & Co of Louisville, Kentucky, which advertised, produced, and sold (for $17 each, quite a reasonable price for this time) devices from 1887 until 1890 by the name Madden Adding Machine (see the photo below).

Madden Adding Machine from 1887 (Courtesy Nico Baaijens, www.calculi.nl)
The machine was a metal, brass, and plastic device, with dimensions: 5.3 cm x 13.3 cm x 8.5 cm.
The nine keys with plastic key covers for entering the numbers are arranged in two rows and are attached to the levers, which have from 1 to 9 teeth. When a key is pressed, these teeth will be engaged with the openings of a rod, which is placed to the length of the box, and the rod will be rotated to an angle, according to the number of the teeth.
To this rod is attached a digital wheel. The tens carry mechanism can perform a carry to the second and third wheel, so the result mechanism is 3-positioned with a maximum value of 999. Left of the wheels is a lever-driven tack and pinion zeroing mechanism.
The segmental gear racks, are normally out of mesh with the pinion, and are fast to the key levers, in such a manner that the first depression of the key causes its rack to rock forward and engage with the pinion, and further depression moves the rack upward and rotates the pinion and units numeral wheel.
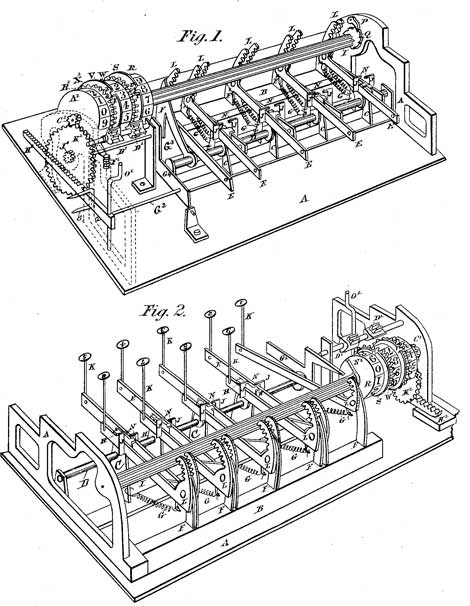
The patent drawing of the Bouchet’s machine
The Bouchet’s machine was manufactured and sold to some extent, but never became popular, as it lacked capacity. Machines of such limited capacity could not compete with ordinary accountants, much less with those who could mentally add from 2 to 4 columns at a clip. Aside from the capacity feature, there was another reason why these single-order machines were useless, except for those who could not add mentally.
Multiple forms of calculation, that is, multiplication and division, call for a machine having a multiplicity of orders. The capacity of a single order would be 9×9, which requires no machine at all, as every 7 y.o. child knows. Multiplying multi-digital numbers, however, is a different thing, and it requires a multiple-order calculator.
After the three first key-operated calculating machines in the world, invented in Europe (see machines of James White, Luigi Torchi, and Jean-Baptiste Schwilgué), there are a number of patents issued in the United States on machines of this class, besides the devices of Parmelee from 1850, Hill from 1857 and Winter from 1859, already examined in this section.
Let’s mention only the St. Louis engineer Leonard Nutz (from 1858), David Nelson (1860), Gilbert Chapin (1870), William Robjohn (1872), David Carroll (1876), Borland & Hoffman (1878), Peter Forrester (1881), Fawcett Plumb (1882), Walter Snelling (1882), Albert Stettner (1882), Spalding (1884), Lawrence Swem (1885), Peter Lindholm (1886) and others. All of these machines varied in construction, but not in principle. Some were really operative and others inoperative, but all lacked what may be termed useful capacity. Some of them are even preserved to the present time.
Such machines, of course, never became popular because of their limited capacity, which required many extra movements and caused mental strain without offering an increase in speed of calculation as compared with expert mental calculation.
It seems strange that up to 1887 the only operative key-driven machines were single-digit adders and nobody managed to invent and produce a multi-column device. It is folly to think that all these inventors never had the thought or wish to produce such a machine.
It is more reasonable to believe there was not one of them, who did not have the wish and who did not give deep thought to the subject. There is every reason to believe that some of them tried it, but there is no doubt that if they did it was a failure, or there would be evidence of it in some form.
The image featured at the top of this post is ©Unknown author / public domain
