The Machine Arithmetique of de Lépine

In the published in 1725 issue of the official publication of the French Academy of Sciences—Machines et inventions approuvées par l’Académie royale is described the calculating machine (machine arithmetique) of one de Lépine (also spelled de l'Epine). Who was de Lépine?

Virtually nothing is known about this person. An astronomical clock, made around 1710 by one Jean Lépine, a Parisian watchmaker, was described at the time in the collection of Buckingham Palace. Moreover, there is a revolutionary and inventive French (actually Swiss) watchmaker from 18th century with the same name, which was fully capable to create such a device—Jean-Antoine Lépine (1720-1814). Jean-Antoine Lépine was considered to be one of the greatest watchmakers of all times, but in 1725 he was only 5 and still lived in the house of his parents Philibert Lépine (Depigny), also a watchmaker, and Marie, née Girod, in Challex, a small village a few kilometers north of Geneva, so obviously he cannot be the inventor. Jean-Antoine Lépine used to use the same inscription "LEPINE – INVENIT ET FECIT", which can be found on one of the calculating devices, mentioned below.

The other strange fact, is that in the description of the Machine Arithmetique of de Lépine is mentioned the machine of Hillerin de Boistissandeau, which will be described in the 1730 issue (5 years later) of Machines et inventions approuvées par l'Académie royale. May be something is wrong with the chronology of the publications?

The Arithmetical Machine of de Lépine (lower left device), together with several Pascalines (© CNAM, Paris)

The Machine Arithmetique of de Lépine was obviously inspired by the Pascaline. It seems several working copies had been manufactured, because at least two of them are still preserved to our time. The smaller one, an 8-digits device, is kept now in the collection of CNAM museum in Paris (see the upper image), while the bigger, a 20-digits device (see the lower image) is in the National Museum of American History in Washington. The machine in Washington is inscribed "DE LEPINE – INVENIT ET FECIT – 1725", meaning that the machine was invented and manufactured by Lépine in 1725.

The Arithmetical Machine of de Lépine (© National Museum of American History in Washington)

Let's examine the variation of the device, described in the publication of the French Academy. The machine is a 12-digital adding device, made by brass and wood, with dimensions 6 x 13 x 34 cm. The rightmost two dials are used for adding of sols and deniers (french monetary units at this time, 1 sol is equal to 1/20 of the livre, 1 denier is 1/12 of the sol) and are divided into 12 and 20 parts. Next ten dials are decimal.

The Arithmetical Machine of de Lépine, front view

The wheels are arranged in two rows. The tens carry from the 6th (last of the lower row) wheel to the 7th (first in the upper row) dial is performed by means of a mechanical system (marked with L in the lower figure), which consists of two small rods (marked with 1), two springs (2) and a clamp (3). On every full revolution of the 6th wheel one of the pins (which is prolonged) raises the lower clamp, and pushes the side clamp, which rotates the 7th wheel to 1/10 revolution. The two springs and the clamp sidelong are destined for fixing and supporting.

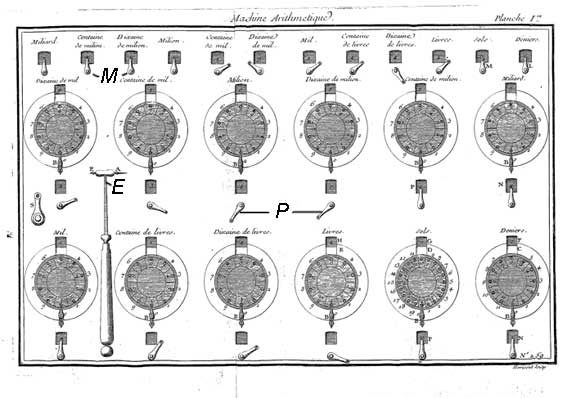
The 12 wheels in the upper part of the machine are not connected one to another and can be used for storing of the intermediate results. In the lower figure can be seen the fixing mechanism of each wheel, which consists of a spring and a clamp (marked with P1 and P2) (the fixing mechanism of the lower wheels (which are destined for the showing of the result) is manufactured in the same manner). The rotating of these wheels can be done by means of clamps M (see the upper figure), which are connected with the axes of the wheels and are rotating by means of the stylus E. Over the windows, where can be seen inscribed over the periphery of the wheels digits, are inscribed the proper units—deniers, sols, units, tents and so on to the billions.

The stylus E actually has 2 edges—short and long. The entering of numbers is done by rotating of the dials, which are divided to 12, 20, 10 and so on parts. Bellow each one of these dials is mounted another dial, which has the same number divisions. Over the periphery of the lower disks are inscribed digits, whish can be seen in the windows, situated over the disks and are used for showing of the entered number.

If in the openings of the dial is pushed the long edge of the stylus, then it will be rotated together with lower disk. If it is pushed the short edge of the stylus, then it will be rotated only the upper disk, but lower disk, showing entered number, will remain static.

The result is presented in the two rows of windows, which are places over the entering dials, where can be seen 12 smaller disks F. Transfer of the digits from the entering dials to these wheel is made by a system of clamps and springs. The tens carry is done by means of a similar system.

Over the periphery of the disks F, which are placed bellow entering dials and are showing the entered number, actually are inscribed 2 rows of digits. The first row is used during the adding, the second (its digits are complement to 10 of the first row)—during the subtraction. Only one of the rows can be seen at a particular moment, and which row can be seen is determined by the clamp S, which can be seen in the left side of the figure. Rotating this clamp, we can show one or another row, depending on if we want to add or to subtract. The resetting of the result to 0 can be done by means of clamps R, which are similar of clamps M, used for entering the numbers in the recording mechanism.

Arithmetical machine of de Lépine, back view

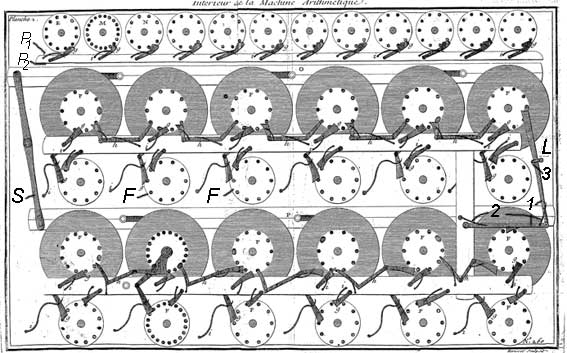
It seems the machine of de Lépine possesses all the defects of Pascaline—the mechanism does not offer reliable transmission (carrying) of the units into the tens, the tens into the hundreds, etc. In it however the small barrels of Pascal are not used.