
The Calculating Machines of Sir Samuel Morland
The polymath Samuel Morland (see biography of Samuel Morland), was a notable English academic, diplomat, spy, inventor, and mathematician of the 17th century, credited with early developments in relation to computing, hydraulics, and steam power. He is an important person for this site because in the 1660s he devised a total of three calculating machines — one for trigonometry (1663), one for addition and subtraction (1666), and one for multiplication and division (1662). Morland’s calculating machines became rather popular and London instrument-makers were still selling Morland’s calculators as late as 1710.
Morland entered government service in 1653 when he was chosen to accompany a British diplomatic mission to the court of Sweden’s Queen Christina. The Swedish Queen was a noted patron of the sciences, and it was most likely at her court that Morland first became acquainted with the Pascaline, the calculating machine of Blaise Pascal, who had presented Christina with an example in 1652. This is probably the most important reason, that some 10 years later, Morland commenced the construction of three calculating devices.
In his book — The description and use of two arithmetick instruments, published in 1673 in London, Morland described two invented calculating devices, which are working without charging the memory, disturbing the mind, or exposing the operations to any uncertainty. This is the first book on a calculator, written in English, and the first separate work on the subject after Napier’sRabdologiae. There was little else in English on calculating instruments for more than 160 years from this book and the publication of Babbage in 1827. The book may also be considered the first comprehensive book in computer literature, as Blaise Pascal published nothing about his own machine, except an 18-page pamphlet in 1644.

The arithmetical machines of Morland were devised between 1662 and 1666 and were presented to King Charles II and the general audience. The first machine (see the photo below) is a simple adding device, similar to the Ciclografo of the Italian Tito Livio Burattini, produced in the late 1650s.

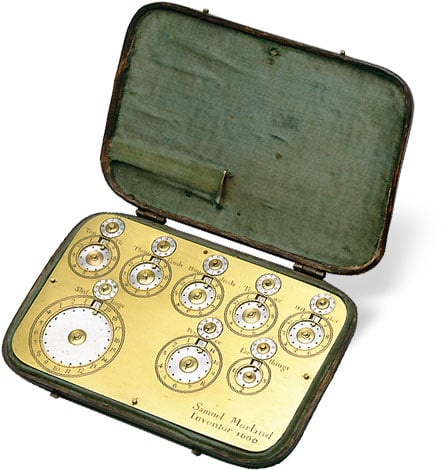
Four examples of the adding machine survive. The largest models can add up to one million, in either decimals or pounds, shillings and pence.
The device (materials used are silver and brass), presented a true pocket calculator, measuring only 4 by 3 inches and less than a quarter of an inch thick (122 x 71 x 8 mm). On page 12 of the book Morland advertises that the instruments may be ordered from Humphrey Adamson, living at Jonas Moore’s house in the Tower (Sir Jonas Moore was an English mathematician, surveyor, ordnance officer, and patron of astronomy, who warmly recommended the machines of Morland). Humphrey Adamson was a very skillful English clock- and instrument-maker.
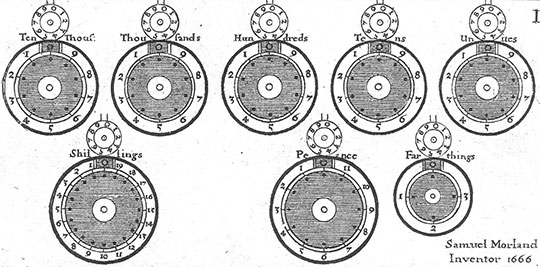
On the lid of the device are mounted 8 pairs of graduated dials. The scales of the dials are inscribed on the ring around them. The lower three scales are divided into 4, 12, and 20 parts and are inscribed and used for calculations in the English currency units of the 17th century — guinea (which was equal to 20 shillings), shilling (which was equal to 12 pennies), and penny (which was equal to 4 farthings). The upper five big dials have decimal scales and are inscribed with words unit, tens, hundreds, thousands, tenth
Across the periphery of each big dial are made openings, according to the scale of the dial — 4, 10, 12, or 20. In this openings can be put a stylus, and the dial can be rotated. During this rotation, in a little window in the upper part of each scale can be seen the appropriate number. Below each window is mounted a stop-pin, which is used for limiting the rotation during the adding operation. Over each big dial is mounted a smaller one, which serves as a counter of the revolutions of the big dial. For that purpose a one-toothed gearing is used — the lower dial has one tooth, while the upper dial has ten teeth, so making a full revolution of the lower dial has as a result 1/10 revolution of the upper one.
The adding operation is performed by rotating the appropriate dials in the clockwise direction, pushing the stylus into the opening against the appropriate number, and turning the dial until the stylus is stopped by the stop-pin. The subtraction can be done by rotating dials in the counter-clockwise direction, pushing the stylus in the opening below the window, and rotating the dial until it moves below the appropriate number.
The machine doesn’t have a tens carry mechanism, and this made it useless for practical needs. In 1668 Morland published a short description in a London newspaper, trying to market it, but without success.

The second of the calculating machines of Morland—the so-called multiplication machine (see the upper photo), is based on the principle of Napier’s bones. The device was described in the above-mentioned book of Morland under the name Cyclologica (see the image below).
Morland ordered the manufacturing of the device to the famous English mechanicians Henri Sutton and Samuel Knibb, and this particular machine was donated by Morland himself to Grand Duke Cosimo III de’ Medici in 1679. The dedication to the Grand Duke contains an obvious error: it gives 1666 as the year of invention and 1664 as the year of manufacturing. Let’s examine the construction of the multiplication machine
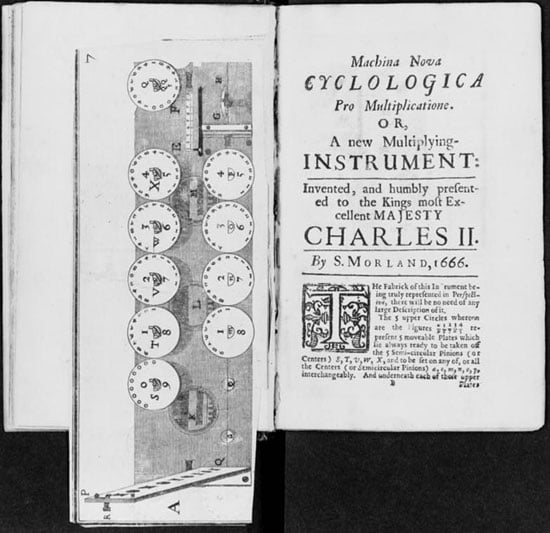
The device is elaborated by silver, gilt, and silvered brass, wood, and crystal. The dimensions are 18 x 55.5 cm.
Actually, the multiplication machine of Morland simplifies only the intermediate products, using the principle of Napier’s rods. There is no automatic or mechanical carry mechanism provided.

The digits from the ten Napier’s rods are inscribed across the periphery of 10 thin metal disks in such a manner, that units and tens of the rods are placed on the opposite ends of the circle (see the nearby and lower images for a closer view to the mechanism). There are two rows of axes in the device, the upper axis is foxed, while the lower can be rotated. In the row of windows, placed between the two axes can be set numbers, thus it serves as a mechanical memory. To perform a multiplication, the appropriate disk must be removed from the upper fixed axis and mounted to the lower working axis. Each of the lower axes is attached to a small pinion in the body of the machine, and this pinion is engaged with a toothed strip. This strip can be moved in a horizontal direction by means of the key, which can be seen in the lower right part of the lower figure, and its movement is marked by an arrow, which can be moved across a scale.

When the appropriate disks are set (according to the digits of the multiplicand), the lower part of the machine is covered by a lid, which has windows. The key must be rotated by the operator until the arrow comes to the digit of the multiplier on the scale, and during this rotation the toothed strip will move and rotate the pinions, engaged with it. Thus in the lower row of windows can be seen the product. If the factors are multi-digital, then these actions must be repeated until all digits are used.
For example, to multiply 23 by 7, the user would first take the discs for 2 and 3, place them on the central posts and close the door so that in the window the number 23 appears (3 in the left-most window and 2 in the left side of the second pair of windows). Then the user would turn the key until the pin on the slider scale pointed to 7. Each time the key is turned the discs are rotated once, which advances the display of the multiplication table for the selected numbers (2 and 3) by one. The windows are constructed so that a number on the leftmost edge of one disc appears next to the number on the rightmost edge of the next disc. The final answer must be obtained by adding the adjacent numbers in the windows, either with pen and paper or, as the inventor suggested, with the help of his instrument for addition. So, to finish the example, after the discs 2 and 3 have been rotated 7 times, the numbers in the display window would read: 1 4 2 1. The final result is found by adding the adjacent digits to give 161.

Besides the two above-mentioned calculating devices, in 1663, Morland invented a third one. It was a device, that could be used for trigonometric calculations (see the nearby photo), which he called the Maccina Cyclologica Trigonometrica. The trigonometer allowed the operator to perform trigonometry by drawing out a problem and measuring the solution as with drawing instruments but without the need for pen and paper. It was a set of three rulers set into a divided circle that could be moved about using dials to form a triangle of any shape.
On 16 April 1668 Morland first printed short descriptions of the two adding devices in the London Gazette. As would now be expected, the instrument made its way into the pockets of modern young gentlemen (at a price of £3 10s).
Despite the excellent workmanship of the arithmetic devices of Morland, they were not very useful for practical needs, moreover, some of his contemporaries were not so fascinated by their usefulness also. Samuel Pepys (formerly Morland’s tutee at Cambridge,) wrote in his 1667-8 years diary, that the machine of Morland is very pretty, but not very useful, while the famous scientist Robert Hooke, wrote in his diary for 31 January 1673: Saw Sir S. Morland’s Arithmetic engine Very Silly. The machines of Morland were, however, appreciated by King Charles II and Cosimo III de’ Medici, Grand Duke of Tuscany, which was more important for Morland as a typical courtier–inventor.


