Pascaline Calculator History
Blaise Pascal invented the Pascaline Calculator. Pascal was considered a child prodigy and was gifted in a variety of areas including mathematics, philosophy, and theology. Pascal’s father, Etienne, held a position calculating taxes. He was often overwhelmed with work. He and his helpers were often up late figuring tax levies using manual calculations and an abacus (counting boards). In 1642 young Blaise designed a calculating machine to help speed up the process.

Blaise Pascal, the inventor of the Pascaline Calculator
©History-Computer.com
The first several copies of the machine didn’t satisfy the inventor. Later on, however, friends of Pascal presented to the Chancellor of France, Pierre Seguier (1588–1672), a prototype of the calculating machine. Seguier admired the invention and encouraged Pascal to continue the development. In 1645 Pascal wrote a dedicatory letter at the beginning of his pamphlet describing the machine, and donated a copy of the machine to the Chancellor, which is still preserved in CNAM, Paris.
Quick Facts
- Created
- 1642
- Creator
- Blaise Pascal
- Original Use
- Simplifying addition, subtraction, multiplication, and division
- Cost
- Unknown
It seems later that Pascal wanted to manufacture his machines as a full scale business enterprise, but it proved too costly. It’s not known how many machines were sold, but the total was probably no more than ten or fifteen. Price may have been the main issue here, though accounts vary significantly.
Pascal continued to experiment, constructing a lot of variants of the machine (later on called the Pascaline or Pascalene). He worked so hard on this machine, it is said, that his mind was disturbed for the next three years. According to his sister, Gilberte, the young inventor’s exhaustion did not come from the labor he put into designing the machine, but rather in trying to make the Rouen artisans understand what it was all about.

Statue of Blaise Pascal in Paris. His invention of the Pascaline made him famous.
©Millionstock/Shutterstock.com
On May 22, 1649, Pascal received a patent, or what was then called a privilege, on the arithmetic machine. The Pascaline soon become well-known in France and abroad. The first public description was in 1652, in the newspaper Muse Historique. The machine was demonstrated to the public in Paris. Pierre de Ferval, a family friend and a mathematics professor at the Royal College of France, agreed to demonstrate the device to prospective customers in his apartment at the College Maitre Gervais every Saturday morning and afternoon. Pascal went to work writing advertising flyers for the invention and asked a friend, the poet Charles Vion Dalibray, to compose a publicity sonnet.
The Polish queen Marie Louise de Gonzague, a high-ranking and keen patron of sciences, asked to buy two copies. Another fan of sciences, Swedish queen Christina desired a copy to be granted to her. Pascal satisfied their desire, but soon after this lost his interest and abandoned his occasions with the calculation machine until the end of his short life.
From some 50 constructed Pascalines, only 8-9 survived to the present day, and can be seen in private or museum collections (4 in CNAM, Paris, 2 in a museum in Clermont, and several in private collections).
Pascaline Calculator: How It Worked
The Pascaline Calculator had metal dials that looked like spoked wheels. Digits 0 through 9 were displayed around each of the wheels. A user would place the stylus, or a small rod, in the space between the spokes and then turn the dial until a metal stop was reached. The mechanism is similar to the way an old rotary dial telephone would work. After redialing the second number that was to be added, the sum of both numbers would show up in the accumulator.
Each dial had a single digit display directly above. This displayed each value for this particular position. A horizontal bar could be slid to the top to hide all the complement numbers. When slid to the center of the device it hid all direct numbers.
The gears of the machine only rotated in one direction, meaning that negative numbers couldn’t directly be added. To subtract numbers, a method called Nine’s Complement was used. There are two primary differences between performing addition and subtraction on the device. This included the position of the display bar and how the first number was entered.
One of the prime aspects of Pascaline’s Calculator is the sautoir. This is what enables the device to carry numbers. Through the influence of gravity, the sautoir moves toward the next wheel. Sautoir is from the French word sauter, that means “to jump.” The carry transfer then moved the next wheel only a single step.
The tens carry mechanism of Pascal’s invention had an advantage compared to Schickard’s Calculating Clock because it needed only a small force for transferring the motion between adjacent wheels. This advantage, however, is paid by some shortcomings. During the carrying, a noise is produced, and if the box is hit, it may cause unwanted carrying.
Carrying numbers in Pascaline’s Calculator consisted of three phases:
- The display register must start with 4 and move to 9. The sautoir lifts and the active wheel would touch what is receiving the carry.
- The second phase begins after the register starts at 9 and goes down to 0. The sautoir is moving up and then, suddenly, the second carry pin will drop it. Its own weight causes the sautoir to fall.
- The third phase consists of a pin pushing against the receiving wheel, causing it to turn. The upper rachet then correctly positions the whole receiving mechanism. During the final phase the sautoir then added 1 to the receiving wheel. During this phase the sautoir wasn’t touching the wheel.
It’s important to note that the machine must be re-zeroed before each new calculation. The following are images and descriptions of the machine and the process.

A Pascaline from 1652 (© Musée des Arts et Métiers, Paris)
©David. Monniaux, CC BY-SA 3.0, via Wikimedia Commons – Original / License
The dimensions of the brass box of the machine (for 8 digital positions variant) is 35.1/12.8/8.8 cm. The input wheels are divided by 10, 12 or 20 spokes, depending on the scale. The spokes are used for rotating the wheels by means of a pin or stylus. The stylus rotates the wheel until it gets to an unmovable stop, fixed to the lower part of the lid. The result can be seen in the row of windows in the upper part, where is placed a plate, which can be moved upwards and downwards. This allows the upper or lower rows of digits to be seen and used for addition or subtraction.
The principle of action of the mechanism is shown in the lower sketch.
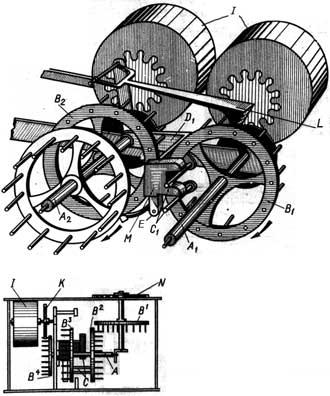
A sketch of the calculating mechanism of Pascaline Calculator
©History-Computer.com
The rotating of the wheels is transferred via the mechanism to the digital cylinders, which can be seen in the windows in the following photo.

A view to the digital cylinders of Pascaline Calculator
©History-Computer.com
The following are several images that provide examples of how the calculator specifically worked.
On the surface of cylinders are inscribed 2 rows of digits in this way, that the pairs are complemented to 9. For example, if the upper digit is 1, the lower is 8. On the lid is mounted a plate (marked with 2 in the lower sketch), which can be moved upwards and downwards and by means of this plate, the upper row of digits must be shown during the subtraction, while the lower one—during the addition.
Before starting a calculus, you shift the sliding cover that lays over the display windows toward the edge of the machine. Then you have to set the marked spokes in order to read “0” on all the drums. This is done by setting the stylus in between the spokes that are marked with white paper and by turning the wheel until the needle stops it. This brings for each wheel the highest digit the drum can have, that is to say 9. Then you turn the last wheel on the right of only one position afterwards all the drums will display 0.
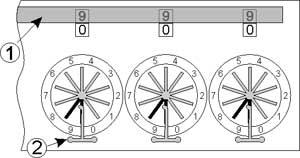
Zeroing of the mechanism
©History-Computer.com
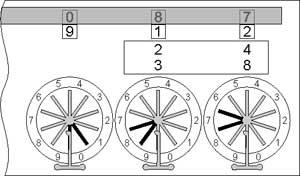
Subtraction will be a little more difficult and will require not only rotating, but some mental work. Let’s make, for example, 182–93. After zeroing of the mechanism (to see 000 in the lower windows), the plate of the windows must be moved in lower position. At this moment in the windows can be seen the number 999. Then the minuend is entered as a complement to 9, i.e. the units-wheel is rotated for 7, the tens-wheel for 1, and hundreds-wheel to 8 (the complement to 9 of 182 is 817). As the upper row of digits actually is moved to descending order, thus we have made a subtraction 999-817 and the result is 182 (see the lower sketch).
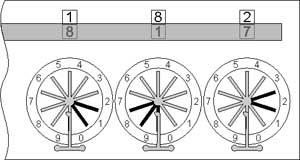
Subtraction with the Pascaline
©History-Computer.com
Then enter subtrahend (93), making a subtraction 182–93 (during rotating of the wheels two carries will happen—during the entering of the units (3), the units wheel will come to 9, and a carry to the tens-wheel will be done, moving the tens-wheel to 7. Then enter 9 to the tens-wheel and it will be rotated to 8, and a carry will be transferred to the hundreds-wheel, making it to show 0. So, we have the right result 182–93=089 (see the lower sketch).
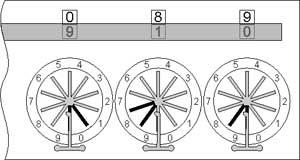
Subtraction with the Pascaline
©History-Computer.com
To be able to use the fastest way for multiplication, the operator must know (or use) a multiplication table. Let’s make the multiplication 24 x 38. First we have to multiply (mentally or looking at the table) units of the multiplicand to the units of the multiplier (8 x 4 = 32) and enter the result 32 in the mechanism (see the lower sketch).
Multiplication with the Pascaline
©History-Computer.com
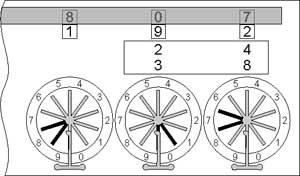
Then, we have to multiply units of the multiplier to the tens of the multiplicand (8 x 2 =16). Then enter the result (16), not in the right most digital positions (for units and tens), but in the next (the positions for tens and hundreds). Then we will have the result 192 (32 + 160) (see the lower sketch).

Multiplication with the Pascaline
©History-Computer.com
Then we have to repeat the same operation for multiplication of the units of the multiplicand to the tens of the multiplier (3 x 4 =12) and for multiplication of the tens of the multiplier to the tens of the multiplicand (3 x 2 = 6), entering the intermediate results into wheels of tens and hundreds (12), and into the hundreds and thousands (06). We have the right result (912) (see the lower sketch).
Multiplication with the Pascaline Calculator
©History-Computer.com
Division with the Pascaline can be done in the way, similar to the manual division of the numbers. First, we have to separate the dividend to 2 parts (according to the value of the divisor). Then we have to perform consecutive subtractions of divisor from the selected part of dividend, until the remainder will become smaller than the part. In this moment we have to write down the number of subtractions. This will be the first digit of the result. Then we have to attach to the remainder (if any) 1 or more digits from the remained part of the dividend and start again the consecutive subtractions, until we receive the second digit of the result. Continue this operation again and again, until the last digit of the dividend will be used. At the end we will have the remainder of the division in the windows, while the result will be written.
Pascaline Calculator: Historical Significance
The Pascaline Calculator is significant because it was the first of its kind developed in the 1700s. Pascal’s work almost certainly inspired other inventors and contributed to other mechanical and calculating devices. Other inventions that followed this particular device where calculating machines developed by Gottfried Wilhelm Leibniz, de Lepine, and Jacob Leupold.
Admittedly, not all impressions from Pascal’s contemporaries were positive. Some were unfavorable, such as the October 1648 letter of the English gentleman traveler Balthasar Gerbier to Samuel Hartlib. Gerbier came upon Pascaline not long after a model in wood was finished, and thought it resembled something invented in England 30 years earlier. (Gerbier most likely meant William Pratt’s Arithmetical Jewel from 1616, a simple calculating instrument, that was nothing more than a variant of the common abacus). Gerbier though found many problems with the Pascaline.
Pascaline was described in many sources. An examples is the 18th century books of Jean Gaffin Gallon—Machines et inventions approuvées par l’Academie Royale des Sciences, depuis son établissment jusqu’a présent; avec leur description (see description of Pascaline from Gallon.)
Up Next…
Learn more about over inventors of calculating machines.
- de Lépine He invented the Arithmetical Machine. Discover how it worked and more facts about this fascinating inventor.
- Who Was Jacob Leupold? Biography, History, and Inventions Leupold is known for his calculating machine, and he is the one who invented the air pump!
- Meet Gottfried Wilhelm Leibniz – Complete Biography Leibniz was known by many as “the father of computer science.” Find out why here.
The image featured at the top of this post is ©David. Monniaux, CC BY-SA 3.0, via Wikimedia Commons.