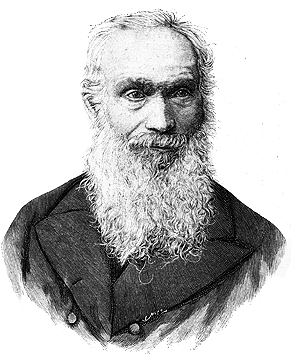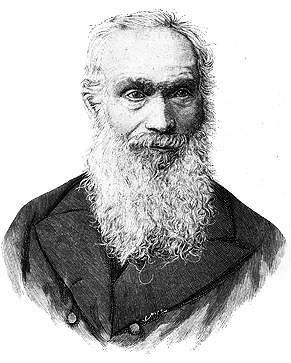
Izrael Abraham Staffel
The Polish Jew Izrael Abraham Staffel was born in 1814 to an impoverished family in Warsaw, Poland, then part of the Russian Empire. His primary education he got at an elementary religious Jewish school, and later entered as an apprentice in a watchmaking factory. There he learned the Polish language, which enabled him to read scientific and technical books and deepen his expertise.
In 1833, when he was only 19, Staffel opened a clockmaker shop in Warsaw (at Marszałkowska str. 125), then he opened another workshop at Grzybowskiej and Gnojnej str., where he worked till the end of his life. Staffel spent most of his life developing various inventions, primarily calculating machines, for which he obtained multiple prizes.
He also invented other devices, such as an anemometer, Ventilator Helis (a powerful fan), a probe for determining the contents of alloys, a counterfeiting machine, and a two-color printing press, used for printing stamps and banknotes (on this machine that printed the first Polish post stamp, the so-called Poland No. 1, in the Stempel Factory in Warsaw). Unfortunately, he did not manage to patent any of his inventions and died extremely poor after a long illness in 1885 in Warsaw.
The distinguished Jewish historian Jacob Shatzky (1893-1956) asserts that Staffel was a relative of Abraham Jakub Stern. If this is true, probably Staffel was inspired by Stern and received from him valuable information about the construction of calculating machines. Anyway, it is hard to believe that the young watchmaker Staffel didn’t know Abraham Stern, who was one of the most remarkable figures in the Warsaw Jewish community during the first decades of the 19th century, and who also used to work as a watchmaker in his youth.
Staffel commenced his occasions with calculating machines around 1835. Still, his first machine, based on pin-wheels of Poleni, was ready in 1842 and was demonstrated at the industrial exhibit in Warsaw as late as 1845 (by recommendation from the Minister Sergey Uvarov (Серге́й Семёнович Ува́ров), and it received a silver medal (now this machine is preserved in the Museum of Technology in Warsaw, see the lower photo). This machine can be used for addition and subtraction only.

Staffel’s machine (property of Muzeum Techniki in Warsaw, Poland)
In 1846, Staffel’s machine was demonstrated and was very positively assessed by the Russian Academy of Sciences in St. Petersburg. Two famous mathematicians, V. Bunyakovsky (later creator of a calculating device also, see Самосчеты Буняковского) and B. Jacobi, gave it a very positive opinion and Staffel was awarded a very prestigious Demidov prize. Later on, the machine was presented to the Russian Emperor Nikolai I, who was so astonished with this invention, that he ordered a sum of 1500 silver rubles to be paid to the inventor.
Later on, Staffel improved his first machine, placing the calculating mechanism on a movable rail, and manufactured a calculating machine for adding, subtracting, multiplication, and division (plus square root). In 1851, the second machine was exposed to the Great Exposition in Crystal Palace in London, where it was awarded a gold medal.
The report, describing the calculating machines presented at the Exhibit, says the following about Staffel’s machine: “The best machine of this kind exhibited is that of Staffel (Russia, 148), which, on examination, seems to combine accuracy with economy of time, and works easily and directly”.
The machine was evaluated higher than the machine of Thomas de Colmar, which was a real sensation. The newspaper Illustrated London News also published an enthusiastic article, with the description of the machine and its picture: “In the Russian Court, modestly secluded amidst the glitter of malachite doors and vases, jewelry and silver, there is one work, the produce of high intelligence, and intended to assist in certain intellectual labors.
This solitary tribute of mind to minds comes not from Petersburg, nor Mexico [meant Moscow], nor from Siberia, nor from the Ural Mountains, but from Poland. We refer to Staffel’s Calculating Machine, №148 in the Catalogue”.

Drawing of the Staffel’s machine in the Illustrated London News
Let’s mention also the description of the machine in the newspaper Illustrated London News
***
The machine is of the size of an ordinary toilet: the mechanism is 18 inches by 9, and about 4 inches high. The external mechanism represents three rows of ciphers. The first and upper row, containing 13 ciphers, is immovable; the second and third, containing 7 ciphers, are movable.
To the right is a semicircular ring, containing the words Addition, Subtraction, Multiplication, Division and Extraction. Underneath is a hand, which serves as a regulator for the operation, pointing ad libitum to either of the four rules or the square root, whichever is to be worked.
The advantage which this machine has above others are as follows:
1. That the four rules and the square root, with fractions, can be worked by means of a curved handle (which in itself is a piece of mechanism), showing the various sums alternatively, without being obliged to note down any auxiliary figure, as is the case with all other calculating machines.
2. That all compound rules, as the rule of three, of five, etc., can be worked by transposition of the regulator, without shifting any of the figures.
3. That, if by subtraction a larger number is subtracted from a smaller, the sound of a bell is heard, indicating the false proceeding; and when turning the handle a negative number shows itself in the upper row, where, instead of the 13 ciphers, the figure 9 will appear in their place, and which, added to the number given, will prove the inverted position of the number. The bell will also be heard if, by division, the handle is turned once too many. A retractive move of the handle will then retrieve the error.
4. That the entire mechanism is of a simple construction, the parts acting without springs, its correctness and accuracy secured, and the efficiency of the mechanism guaranteed.
***
Even many years later, in the Reports of the United States Commissioners to the Paris Universal Exposition, 1867, Staffel’s machine is praised in Chapter XVIII “Metrology and Mechanical Calculation”: Of the numerous calculating machines which have been proposed or constructed since that of Mr. Thomas became an ascertained success, those of Messrs. Maurel & Jayet of France, and of Mr. Staffel of Russia, are the only ones which, so far as is known, have solved the problem in a manner entirely satisfactory
Staffel invented also another, a simpler calculating machine, used for adding and subtraction (see the picture below), similar to the machine of Kummer. This machine is now preserved in Braunsweig Landesmuseum, Germany.

Staffel’s adding machine (from the magazine Tygodnik Ilustrowany, 1867)
The image featured at the top of this post is ©Unknown author / public domain