Chaim Zelig Slonimski

Chaim Zelig Slonimski

The Polish/Russian Jew Chaim Zelig Slonimski (see biography of Chaim Zelig Slonimski) was a Hebrew publisher, astronomer, inventor, and science author, a prominent figure in this humble website, due to his inventive calculating machines.

Slonimski was born on March 31, 1810, in Byelostok, in the Grodno Governorate of the Russian Empire. His family provided him with a traditional education, and he studied mathematics, astronomy and Hebrew by himself.

In late 1830s Chaim Zelig Slonimski settled permanently in Warsaw as guest in the home of Abraham Jakub Stern, the popular mathematician and inventor of various machines (including calculating). This occurred for the young author and scholar who had recently been divorced, thanks to Stern, who wanted him as a son-in-law for his youngest daughter, Sara Gitel. The match was finalized at the beginning of 1842, one month before Stern’s death. There is no doubt, that Slonimski was heavily influenced by his mentor and father-in-law Stern, but besides this valuable legacy, Slonimski must have been a very smart man, judging by the rest of his life.

Three calculating machines were invented and produced by Slonimski before 1843, one for addition and subtraction, one logarithmic device, and one for multiplication. The first account of his calculating devices is from September 1839, when he wrote to a friend, that he had built a calculating machine and that he was working on a 20-digit logarithmic device.

It seems Slonimski demonstrated firstly the adding machine, because in the June 1840 issue of the Vilnius newspaper Kuryer Litewski was announced (at that time Slonimski was in Vilnius to publish his mathematical handbook):
A Jew Slonimski born in Bialystok, recently invented a small machine for calculating, which thanks to its dimensions (length 10 inches, width 3 inches and 1 inch height), comfort, and low price deserves to be widely used. Everybody who knows digits only can, with the help of this machine, make calculations easily, fast, and without need to think. This machine can be seen at the inventor’s residence, where he is now working on a new machine for calculating logarithms. With the help of this machine one can simply and comfortably find the differences of Bruget logarithms,as well as natural logarithms up to 14 decimal digits

The adding machine was presented also in 1841 in Königsberg, where Slonimski was invited through the recommendation of Bessel, the great astronomer, who taught at the university. Slonimski got permission to expose for inspection, in the university building, his calculating machine and had the pleasure to see it highly approved by the whole faculty. Slonimski obviously described (or demonstrated) his logarithmic device also, because there is a letter from Carl Gustav Jacobi to his brother, asking for support for Slonimski to demonstrate it in St. Petersburg.

The multiplication machine was based on a newly discovered theorem from number theory, called the Slonimski Theorem. The operation of the multiplication machine, which is more important, has been described by Slonimski himself in Russian. In principle, it was an implementation of multiplication tables, which resulted from application of the Theorem. Since the amount of related numbers was not that large, they were put on the cylinders, which—when moved appropriately—were showing the multiplication results in small windows.

Slonimski’s machines got high recognition during his life time. In August, 1844, he brought his machines to Berlin, where he demonstrated them first to some prominent scientist as Alexander von Humboldt, Friedrich Bessel, Johann Encke, and others, then to the Royal Prussian Academy of Sciences, and his work was highly appreciated. The accurate results of his machines gained him here the same approbation, and although he did not communicate the theoretical principles on which the whole rests, yet, Humboldt recommended him to the Friedrich Wilhelm IV, King of Prussia, where he saw, at his representation, his machines highly approved. Humboldt even intended to provide him with material means so that he could settle in Berlin and then occupy the chair of mathematics in one of the Prussian universities, but family circumstances prevented Slonimski from taking advantage of this offer.

In the same 1844, Slonimski published an article on calculating machines in the Journal für die reine und angewandte Mathematik, vol. 26, 1844, pp. 184–190 (see the article of Slonimski). In 1845 an article “Selig Slonimski and His Calculating Instrument” was published Illustrierte Zeitung, Leipzig, vol. 5, no. 110, 1845, pp. 90–92 (see the article for Slonimski).

Next year, in April of 1845, he presented the multiplication machine to the Academy of Sciences in St. Petersburg, and obtained its recommendation for the Demidov Prize of the Second Grade. The Second Grade prize amounted to 2500 Rubles. For comparison, one should say that a university scholarship of 20 Roubles per 1 month could easily cover a student’s living and educational expenditures. This prize was awarded to him on 24 June, 1845. Moreover, the President of the Academy, Minister von Uwaroff, presented the inventor before the Emperor, and a few days afterwards the following Ukase appeared:
“Ukase to the Senate.
“The Hebrew, Selig Slonimski, born in the city of Bialystok, is hereby, in approval of the high merits which his learned and useful labours in the Mathematical branch have gained, raised to the rank of an Honorary Citizen.
“Nicolas I.
“Peterhof, 26th July, 1845.”

In 1847 Slonimski applied for a patent in USA (see the petition of Slonimski), stating that there was a company in New York— Neustadt and Barnett (of two Jews from Warsaw named Samuel J. Neustadt and David Barnett), who were interested in financing his invention and they apparently paid $300—at that time a very large sum of money—in order to get a patent. For unknown reason, this application was unsuccessful. Barnett managed however to obtain a Great Britain patent on Slonimski’s behalf for the adding device and the third model of his multiplying device (British patent number 11441 of 1847). By a stroke of luck Slonimski managed to sell the rights of the manufacture of his adding machine to England for £400. He invested the money in the acquisition of a fruit orchard in the town of Tomashov.

The theorem of Slonimski is derived from the Farey numbers (a sequence of the irreducible irrational numbers a/b where b<=n, which belongs to the segment /0, 1/ and is arranged in increasing order). Using this theorem, Slonimski composed a table with 280 columns, each of which contained 9 numbers. The table was engraved on the cylinders; as the main component of the device, these cylinders can both revolve around the axis (the shaft) and move (reciprocate) along it. Aside from the main cylinders, there are also 2 small cylinders with digits from 0 to 9 on one of them and the letters a, b, c, d, together with digits 1 to 7 on the other. The cylinders are driven with the use of handles, fastened to the shaft end. While the small cylinders are immobile, the main cylinders are moved along their axis with toothed gearing, driven with screws, mounted on the cover. There are also handles on the cover, which set the numbers (multiplicands).

Slonimski’s multiplying machine (in the right side is shown a single cylinder from the multiplying device).

The whole instrument is made of a flat wooden box, similar to a chessboard, 40 cm long, 33 cm wide and 5 cm high. On the cover of the machine, there are 11 rows of windows. The first (lower) window shows the multiplicand. When the number is set in the first row, both letters and numbers appear in the windows of the second and third rows. Their combination is the code, which informs the operator which screw should be turned (and which cylinder is to be shifted). After this, windows 4-11 show the resulting numbers. The 4th row shows the product of multiplication by 2, the 5th by 3, the 6th by 4, etc. Finally the products of all ranks are displayed. After adding them on paper, the desired product is obtained. Apparently, the convenience of this method was rather questionable, and it is no wonder, that there is no evidence of its systematic practical use.

More importantly, this machine was the only available device for discrete calculating. The basic principle of its work was the theory of numbers, rather than complicated mechanism alone. It was the mathematical art of the device, which was so highly appreciated by the Academy, and personally by the famous mathematician Ostrogradsky. As the Academy report noted, “the discovery of the basic feature of multiple numbers was the principle but not the only condition for composing this calculating machine… The inventor also should arrange the aforementioned 280 types in a proper order and also invent a phantom key (the code). Finally, the surface of each of the six cylinders is covered with complicated system of 2280 numbers and 600 letters with indicators. This artificial ordering demonstrates the shrewdness of its author’s mind, which raises Mr. Slonimski’s device to the level of an analytical mathematical instrument. It is not just a calculator, of which the main idea is represented by the numbers of its pinions.”
The Academy commissioned Slonimski to publish the proof of his theorem, together with a detailed description of the machine in Russian language. The task was performed within a short time, and the book appeared in 1845.

Later on, other inventors made similar devices—August Leopold Crelle, Henry Knight, Herschell Filipowski. In 1881, a Russian Jew—the mathematician Zebi Hirsch Joffe, created a popular counting tool (a set, consisting of 70 rectangular bars with totally 280 columns on all sides), named Joffe’s Counting Bars, based on the Slonimski’s theorem.

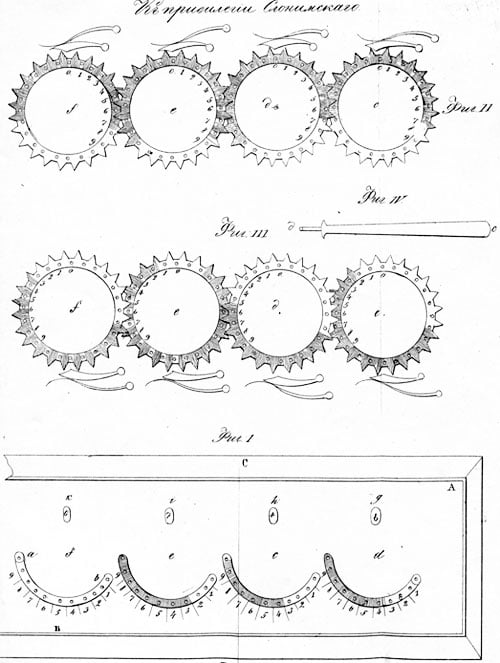
For his calculating machine for addition and subtraction, the so called arithmetical machine (see the patent drawing below), Slonimski also obtained a patent (Привилегия Слонимскаго) on 24 November, 1845, for the period of ten years (see the patent of Slonimski RU1845-11).

The patent drawing of Slonimski’s adding machine.

A working example of Slonimski’s adding machine, made by the Warsaw mechanic and optician Jakob Pik, survived to the present and is kept in the collection of Museum of the Jagiellonian University, Poland (see below the lower photos of the device).

The adding device consists of two rectangular brass plates, in which there are curved incisions showing wheel dials. It has seven 24-teeth wheels, which can be rotated by means of a stylus, each corresponding to one decimal position. Windows above the incisions allow the display of results. On one side, the machine is used for additions (top plate), and on the other side, it is used for subtractions (back plate).

On the circumference are drilled 24 holes, appearing across the digits, and permitting the operator to advance the wheels by from 1 to 9 units with the use of the stylus. A ribbon spring above each wheel, composed of a band, stops the uncontrolled advancement of the wheel. The teeth located between the wheels partially overlap, an important detail for the transmission of a carry. They are alternately placed above or below each other depending on the side that is used.

Slonimski’s design has a significant flaw—tens carry needed to be manually transmitted for each position, and if the operator was not careful, mistakes could be made.

Slonimski’s adding machine (© Museum of the Jagiellonian University, Poland).

Despite its flaws, it seems Slonimski’s adding device had a significant impact on the development of calculating devices, because only a year later, after Slonimski received a patent in St. Petersburg for his adding device, Heinrich Kummer designed in the same St. Petersburg a slide adder or what it’s now called a Kummer or Troncet type adder. The slide adders of this type became the most popular adding devices, and were manufactured more than a century until the mid-1970s.

It seems after selling the rights to his calculating devices in 1847, Slonimski was no longer developing them, and transferred his efforts to other inventions.

Up Next…

Plenty more inventors to read about below!

• Johannes Gutenberg: One of Earth’s Most Important Inventors. The invention of the movable-type printing press allow books to be printed with much faster speed than ever before.
• Meet Nikola Tesla – Complete Biography, History, and Inventions. Tesla had a mind that was way ahead of his time!
• Meet Albert Ludlum – Engineer, Inventor, and Business Owner! Ludlum created devices for use in addition but also mining and dredging.

The image featured at the top of this post is ©G-Stock Studio/Shutterstock.com.