
Philipp Matthäus Hahn
The cylindrical calculating machines of the German parson Philipp Matthäus Hahn (see biography of Philipp Matthäus Hahn) were the first fully functional popular four-species mechanical calculating machines (the earlier machines of Braun remained relatively obscured and unknown to the public).
Philipp Hahn was a skillful mechanician, who was engaged in making clocks and planetariums. He needed a calculating device, in order to calculate the parameters of his machines, that’s why sometime in the summer of 1770 he started to design a calculating machine. The first working copy of the device was ready in 1773 but was demonstrated as late as 1778 because Hahn had difficulties with the reliability of the tens carry mechanism.
Until 1779 four machines were made, till the end of his life, Hahn manufactured about 5-6 devices, and only two of them survived to the present. After his death, several calculating machines by his design were created by his apprentices, in the photo below you can see a variety of Hahn’s machines, made by Johann Christoph Schuster, an apprentice and brother-in-law of Hahn.

A copy of the calculating machine of Hahn (made by Johann Christoph Schuster)
Hahn certainly has been acquainted with the machine of Leibniz (not only from Theatrum arithmetico-geometricum of Leupold, but also from other sources), and that’s probably the reason to use the stepped drum of Leibniz in the construction of his device. The arrangement of the device has also some similarities with Leupold’s calculating machine.
In an article in the magazine Teutschen Merkur from 1779, Hahn mentioned that:
When my time was occupied with making astronomical clocks, I had to deal with calculations of long fractions, multiplication and division of large numbers, and I was so overwhelmed, that my primary work was close to be stopped.
Then I recalled that some time ago I read a book for Leibniz, which mentioned his calculating machine, for which he spent a lot of money, without satisfactory result. I decided to spare some time in this direction. Certainly, I also wasted much time and money experimenting and troubleshooting the construction of my device. Finally, I managed to construct a rather advanced and reliable machine. Most difficulties I met during the construction of the tens carrying mechanism
Hahn needed quite some time to solve the problem with the tens-carry mechanism (he complained several times about the poor quality work of his mechanicians), but he managed to resolve it, partly by changing the initial rectangular form of the machine with a circular. So the first working copies of the machine had ten digital positions, and the latter had 12 digital positions.
The main part of the mechanism of each digital position is a small stepped drum (see the staffelwalze in the lower drawing), mounted on an axis, which can be moved upwards and downwards.
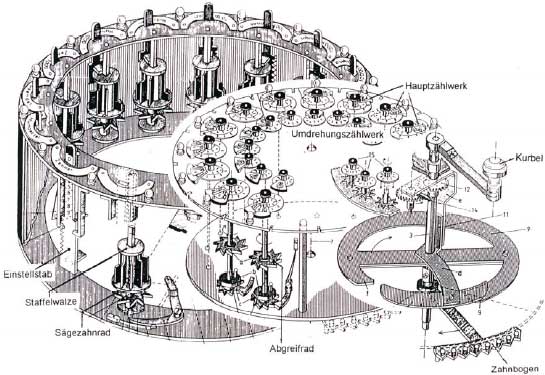
The calculating machine of Hahn, a drawing
During the rotation of the mechanisms of the machine by means of the handle in the middle of the lid, a stepped drum will be engaged with the wheel of the main counter, which is also attached to vertical axes, and according to the vertical position of the appropriate stepped drum, the wheel will be rotated to 0, 1, …, 9 teeth.
The dials are graduated with two scales. The outer ring of digits is black and is used during adding and multiplication, the inner one is red and is used during subtraction and division. The digits of the inner scale actually complement to 9 of those in the outer scale (i.e. below 0 is 9, below 1 is 8, etc.).
The entered in the input mechanism (the stepped drums) number is transferred to the main counter by rotating of the handler. There is also an additional counter, which counters the revolutions of the handle. The module of the additional and main counter is separated by the calculating module (module with the stepped drums) in a separate ring.
This means, that the calculating mechanism is separated by the displaying mechanism. Thus, by rotating the ring of the counters, we actually can move the multiplier (divisor), during the multiplication (division). This moving can be controlled by a special arrow-pointer.
An adding operation can be done as follows:
1. The dials must be set to 0 (if it is necessary). By rotating the axes of the main counter, we set the first addend in the bigger dial (with black digits).
2. Then by pulling the axes of the stepped drums we set other addend.
3. By rotating of the handle to 1 revolution, the number is transferred to the main counter and the result can be seen in the windows of dials.
The subtraction can be performed in similar way, but the minuend is set according to the red digits, while the subtrahend is set by pulling the axes of the stepped drums. After the rotating if the handle to 1 revolution the result can be seen in the windows of dials.
The multiplication can be done (by performing successive additions) thus:
1. The dials must be set to 0 (if it is necessary). The multiplicand is set by pulling the axes of the stepped drums.
2. The handle must be rotated to the revolutions, equal to the number of the units of multiplier (the number of revolutions can be seen in the small dials).
3. Then we have to multiply the multiplicand by the tens of the multiplier, so we have to shift the multiplicand one digital position to the left, by rotating the ring with the dials.
4. The handle must be rotated to the revolutions, equal to the number of the tens of multiplier.
5. If it is necessary, the same actions must be repeated for hundreds, thousands… of the multiplier.

Another copy of the calculating machine of Hahn, made by Johann Christoph Schuster in Ansbach between 1805 and 1820 (© Arithmeum Museum, Bonn)
The division is done in a way, similar to multiplication, but in this case, are used the red digits of the dials and it is based on successive subtractions.
The calculating machine of Hahn became popular in Germany in the end of the 18th century and was demonstrated to the Emperor and described in the press.
It is known also that Hahn designed and manufactured several simple adding machines, which he sold during his lifetime. These devices were used for monetary calculations (for mechanizing the changeover between Kreuzer and Gulden, where 1 Gulden = 60 Kreuzer). Unfortunately, none of these survived to our time, there is only one copy of a machine, attributed to Hahn, kept now in the collection of Arithmeum Museum, Bonn (see the lower photo).

A replica of the adding machine of Hahn (© Arithmeum Museum, Bonn)
The adding device in Arithmeum has brass and steel mechanism, put in a leather-covered wooden box. It has six dials in a row, and the dials are set by means of a stylus. Obviously, only addition is possible, as there is no inscription for complemented to 9 digits.
The dials are returned to zero by turning them backward. The tens-carry mechanism is simple but fully functional. Later one of Hahn’s apprentices, Jakob Auch, created a similar machine (see machine of Auch), but with an improved tens-carry mechanism.
The construction principles of Hahn’s machines were continued by his eldest son, Christoph Matthäus Hahn (1767-1833), who worked as a court mechanic in Stuttgart, by his apprentices Jakob Auch (1765-1842) and Johann Christoph Schuster (1759-1823, he married one of Hahn’s sisters), by brothers Sauter from Esslingen (Johann Jacob Sauter (1843-1803) had been an apprentice and journeyman at the workshop of Hahn), and by his friend and schoolmate Philipp Gottfried Schaudt (1739-1809).
The image featured at the top of this post is ©Unknown author / public domain
