Viktor Bunyakovsky was a renowned Russian mathematician who lived in the 19th century. He introduced several new mathematical concepts but is best known for his numerous contributions to number theory. Throughout his career, Bunyakovsky published over 120 research papers, and his works covered an array of mathematical topics, including geometry, algebra, and analysis. His contributions to number theory have enriched the field of mathematics and continue to inspire new avenues of research to this day.
Who was Viktor Bunyakovsky?

Viktor Bunyakovsky was a famous Russian mathematician. He was also known as a member and vice president of the Petersburg Academy of Sciences.
Quick Facts
- Full Name
- Viktor Bunyakovsky
- Birth
- December 16, 1804
- Death
- November 30, 1889
- Nationality
- Russian
- Place of Birth
- Bar, Podolia Governorate, Russian Empire (now Ukraine)
- Fields of Expertise
- [“Mathematics”,”Physics”,”Science”]
- Institutions
- St. Petersburg Academy of Sciences
- Contributions
- Catchy-Schwarz inequality, Bunyakovsky Conjecture, probability theory, number theory
The mathematician is acknowledged for his significant contributions to probability and number theories. And in 1859, he was credited for his early discovery of the Cauchy-Schwarz Inequality.
Bunyakovsky also stood out as one of the best mechanics of the time. Through his mechanic job, he invented numerous devices, such as the pantograph, planimeter, etc.
In 1828, Bunyakovsky came up with a review of the types of the abacus, developed by the mathematician general Svobodsky. Through that, Bunyakovsky developed an interest in calculating devices.
While working on that, Bunyakovsky put more effort into the problem of tens carry, intending to develop a device to resolve the issue.
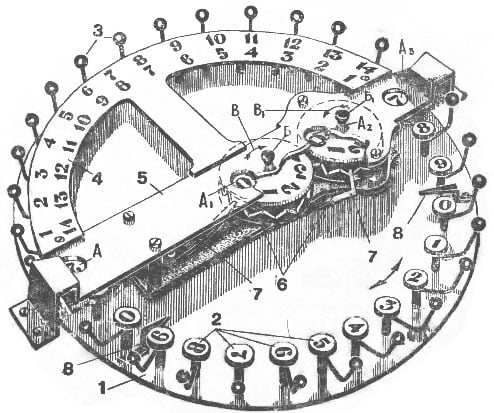
In the mid-1860s, the inventor developed a calculating device, referred to as an automated abacus. On February 14, 1867, Banyakovsky demonstrated his calculating gadget to the academy. Even so, it seems he made only one, which is the original prototype currently preserved at the Polytechnic Museum Collection in Moscow.

Bunyakovsky’s automated abacus consists of the following:
- A meta circle, rotating around its axis freely with three fixed teeth.
- Rods mounted with spherical handles and held together with digits ()). Their work was to turn around the disks ().
- Results digits ranging from 0 to 9 and repeated three times.
- Ratchet wheels.
- A fixed arcuate plank fitted with two numerical rows. The outer row was ideal for additions, while the outer row served subtraction purposes.
- A spring that served as a fixing mechanism.
- The plank with digital disks buttons (6, 6), control window (), and the result windows (, A, A).
When carrying out additions with the automated abacus, the metal circle on the device rotated counter-clockwise. For subtraction calculations, the metal circle moved clockwise. The results would appear on the device windows (, A, A).
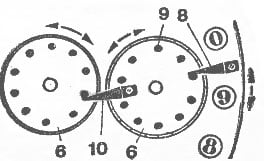
On the other hand, the tens mechanism of Bunyakovsky’s automated abacus consisted of:
- Three teeth fitted with a metal circle that rotated on its axis. It carried up to ten disks.
- Digital disks for hundreds and tens.
- Column openings that were in contact with the tens carry teeth.
- A fitted tooth on disk for tens. It carried hundreds of disks.
Bunyakovsky’s tens carry mechanism device had a limited capacity. The input digits would not exceed number 14, while the results would not exceed 999. The calculating gadget further lacked a mechanism to inhibit the moving parts’ mechanical inertia.
As time went by, Bunyakovsky started to use his automated abacus for scientific calculations. However, no one else made use of the device. Nonetheless, its improved version still exists and has been in use for some time.
Early Life
Viktor Bunyakovsky was born on December 16, 1804, in Bar, Podolia Governorate, Russian Empire (now Ukraine). He was the son of Colonel Yakov Vasilievich Bunyakovsky of a cavalry regiment. Bunyakovysky’s father was murdered in Finland in 1809.
While doing his initial mathematical education, Bunyakovsky was living at the home of Count Alexandra Tormasov, his father’s friend, in St. Petersburg. But in 1820, he decided to travel with Tormasov’s son to a university in Coburg to pursue some studies. Later on, they both proceeded to Sorbonne, Paris to further their studies in mathematics.
While at the Sorbonne, Bunyakovsky had a chance to go for his lectures from Poison and Laplace. His primary focus was on researching and studying his physics and mathematics fields.
In 1824, Bunyakovsky graduated from the Sorbonne, attaining a bachelor’s degree in mathematics. And by the spring of the year 1825, Bunyakovsky continued to research for his doctoral dissertation. In the process, the mathematician managed to write three dissertations under the supervision of Cauchy. The areas of focus were:
- Heat propagation in solids.
- Radius vector determination in elliptical motion of planets.
- The rotary motion with a set of plates of constant thickness, creates a resistant medium.
Luckily, Bunyakovsky completed his dissertation papers on theoretical mechanics, physics, and mathematical physics. Thereafter, he successfully obtained his doctorate under Cauchy-Schwarz’s supervision.
Career
After staying abroad for seven years while pursuing his studies, Bunyakovsky returned to St. Petersburg in 1826. At this place, the mathematician took up the research and teaching role and did it for most of his life.
Apart from lecturing university courses, specifically probability theory, analytical mathematics, and differential equations, Viktor Bunyakovsky was on the frontline in preparing teaching manuals and syllabi for military academies and Russian schools.
He served as a lecturer at the First Cadet Corps (now Naval Academy) from 1826 to 1831, his main fields being mechanics and mathematics. At the same time, Bunyakovsky was also lecturing at the Communications Institute in St. Petersburg.
The years between 1828 to 1864 saw Viktor Bunyakovsky rise to handle officer classes at the Naval Academy. From 1846 to 1880, he became a professor at the St. Petersburg University in Russia.
Besides, Bunyakovsky started to teach mathematics at the St. Petersburg State Railways University in 1859. The naming of the university was after Alexander 1 in St. Petersburg, Russia.
On top of his teaching roles, Bunyakovsky significantly contributed scientific ideas to the probability theory and number theory. He also expressed interest in other science-related matters, such as differential equations, mathematics education, mathematical analysis, and actuarial mathematics.
The mathematician is also the mind behind the Bunyakovsky conjecture, involving the number theory and theoretical mechanics. He also discovered the Cauchy-Schwarz inequality, which he demonstrated for the infinite-dimensional case in 1859.
But that’s not all; Bunyakovsky has risen through the ranks over all these years. In 1828, he became a precursor organization member to the Russian Academy of Sciences.
Furthermore, the mathematician was recognized and named an adjunct in mathematics. Later on, on March 24, 1830, he was recognized as an extraordinary academician.
On April 8, 1864, Bunyakovsky further climbed the ladder to become the vice president of the Russian Academy of Sciences. He served as the vice president for about 25 years, ranging from April 1864 to September 1889.
In 1875, Viktor Yakovlevich Bunyakovsky was recognized and awarded a medal bearing his name for standing out as the best in mathematical research.
What Did Viktor Yakovlevich Bunyakovsky Invent?
Invention 1: Cauchy-Schwarz Inequality
The mathematician patented the Cauchy-Schwarz Inequality, one of the most widely used inequalities in mathematics. The inventor demonstrated it in the infinite-dimensional case in 1859. Later on, Hermann Schwarz improved the project.
Viktor Bunyakovsky Marriage, Divorce, Children, and Personal Life
Net Worth
Although there is much to say about Viktor Bunyakovsky’s achievements and developments, the information about his net worth remains scanty. There is no reliable documentation of the value of his possessions. Besides, details about his marriage, divorce, and children are also not documented.
Marriage
No information is available about Viktor Bunyakovsky’s marriage.
Divorce
No information is available about Viktor Bunyakovsky’s divorce.
Children
No information is available about Viktor Bunyakovsky’s children.
Tragedy
Viktor Banyakovsky died on November 30, 1889, in St. Petersburg, Russian Empire.
Awards and Achievements
Award 1: On May 7, 1828, Banyakovsky was named and recognized as the adjunct in mathematics
Award 2: In March 1830, 24, the mathematician was named an extraordinary academician.
Award 3: Viktor Banyakovsky was recognized and given a medal with his name by the St. Petersburg Academy of Sciences for being outstanding in mathematical research.
Banyakovsky is also celebrated for his notable scientific contributions to probability theory and number theory.
Viktor Bunyakovsky Published Works and Books
Bunyakovsky wrote the book titled Foundations of the Mathematical Theory of Probability and published it in 1846. He also wrote and published more than 150 research works and some books.


