Key Points:
- Thomas Fowler is best known for creating a booklet titled Tables for Facilitating Arithmetical Calculations, which was his attempt to automate mathematical calculations.
- In 1999, Pamela Vass and David Hogan, from North Devon, England hired Mark Glusker, a skillful mechanician, to create a replica of the Ternary Calculating Machine designed by Thomas Fowler.
- The replica was built in 8 months and is currently housed at the Great Torrington Museum.
The Ternary Calculating Machine of Thomas Fowler
During the 1830s the Englishman Thomas Fowler (see biography of Thomas Fowler) became the sole manager and partner of the only bank in Torrington, Devon, Messrs Loveband & Co. He also became treasurer of the Torrington Poor Law Union. The tedious nature of the calculation of payments for each of the parishes, which was one of his responsibilities, led him to attempt to automate the calculations by the use of tables. Fowler’s solution was brilliant and led, in 1838, to Fowler’s Tables for Facilitating Arithmetical Calculations.

©Unknown author / public domain
The tables used a method based on Fowler’s realization that any number might be produced by a combination of the powers of 2 or 3. The first section of the booklet is the Binary Table or a table of indices of the number 2 from 1 to 130048. The second section is the Ternary Table or a table of the indices of the power of the number 3 from 1 to 3985607.
Soon after Fowler had devised the tables, he used the same ideas to build a mechanical calculating machine. This was exhibited before members of the Royal Society in May 1840. In a subsequent letter to the famous English mathematician and astronomer George Bidell Airy, Fowler writes:
This Machine was constructed entirely with my own hands (principally in wood) with the utmost regard to economy and merely to put my ideas of this mode of calculation into some form of action; It is about 6 feet long, one foot deep and three feet wide. In Brass & Iron it might be constructed so as not to occupy a space much large than a good portable writing desk and with powers such as I have described.
The Astronomer Royal, Professor George Airy was to promote Fowler’s invention to a gathering of the British Society for the Advancement of Science in August 1840. In the minutes of that meeting, we read:
“Mr Airy gave an account of Mr Fowler’s new Calculating Machine. The origin of the machine was to facilitate the guardians of a poor-law district in Devonshire in the calculating of the proportions in which the several divisions were to be assessed. The chief peculiarity of the machine was, that instead of our common decimal notation of numbers, in it ternary notation was used; the digits becoming not tenfold but threefold more valuable as they were placed to the left; thus, 1 and 2 expressed one and two as in common, but 10 expressed not ten but 3, 11 four, 12 five; but again 2 can be expressed by three, one taken from it. Now, let T (one with a bar over it), written thus with a small bar above it, mean that it is subtractive; then 12 and 2T are the same in effect, both meaning five; and for a similar reason, by replacing 2 with 1T, we have five written in there several ways; 12, or 2T, or 1TT. The last is the form used it is obvious by an assemblage or unit digits thus positively or negatively written, any number may be expressed. In the machine levers were contrived to bring forward the digits T or 1 as they were required in the process of calculation.”
Fowler writes to Airy:
“I had the honor in May 1840 to submit the machine to the inspection of many Learned Men in London among whom were the Marquis of Northampton, Mr Babbage, W F Baily and A de Morgan Esq with many other Noblemen and Gentlemen, Fellows of the Royal Society etc. and it would have been a great satisfaction to me if I could have had the advantage of your opinion also. They all spoke favourably of my invention but my greatest wish was to have had a thorough investigation of the whole principle of the machine and its details, as far as I could explain them, in a way very different from a popular exhibition: this investigation I hope it will still have by some first rate men of science before it is be laid aside or adopted.
I am fully aware of tendency to overrate one’s own inventions and to attach undue importance to subjects that preoccupy the mind but I venture to say and hope to be fully appreciated by a Gentleman of your scientific achievements, that I am often astonished at the beautiful aspect of a calculation entirely mechanical. I often reflect that had the Ternary instead of the binary Notation been adopted in the Infancy of Society, machines something like the present would long ere this have been common, as the transition from mental to mechanical calculation would have been so very obvious and simple.
I am very sorry I cannot furnish you with any drawings of the Machine, but I hope I shall be able to exhibit it before the British Association at Devonport in August next, where I venture to hope and believe I may again be favoured with your invaluable assistance to bring it into notice. I have led a very retired life in this town without the advantages of any hints or assistance from any one and I should be lost amidst the crowd of learned and distinguished persons assembled at the meeting without some kind friend to take me by the hand and protect me.”
Charles Babbage, Augustus De Morgan, George Airy, and many other leading mathematicians of the day witnessed his machine in operation. Airy asked that he produce plans of his machine but Fowler, recalling his experience with the Thermosiphon, refused to publish his design.
The only depiction of the calculating machine survived to the present time, is in a stained glass window, in St. Michael’s Church in Torrington, Devon, ordered by Fowler’s son. Besides the above-mentioned notices of Fowler, the only other information about his machine is Augustus DeMorgan’s description. DeMorgan saw the abovementioned demonstration of Fowler’s machine in 1840 and described it. Below is the description:
***
The machine consists of four essentially distinct parts. The first, second and third exhibit the multiplicand, multiplier and product, or quotient, divisor and dividend, according as the question to be worked is one of multiplication or division. The fourth is a carrying apparatus, which though at present detached, and employed to reduce the result to its simplest form after the main operation has been performed, might without much difficulty be attached to the multiplier or divisor, and work with it.
Let us now suppose a question of multiplication, both multiplier and multiplicand being exhibited in the ternary system. The multiplicand consists of nothing but a number of rods, each bearing an index, and each movable backwards and forwards. When the indices are all arranged in line, and in one particular line, this multiplicand is 000…. But if any one of the rods be advanced by a certain space forwards, the digit +1 is indicated as occupying the numeral column which that rod represents, and if it be moved the same space backwards, -1 is the digit indicated. This, which we may call the frame of the multiplicand, is thus a collection of rods, not itself connected with any machinery, but only useful as indicating the manner in which the frame of the multiplier is to act.
The multiplier is a frame movable in the direction perpendicular to the rods of the multiplicand and product, and situated between the planes of the two, in such manner that its extremity can be brought by a sliding motion over each rod of the multiplicand in succession. This multiplier consists of a number of rods in a common system, each furnished with two teeth, one at each extremity, the tooth by which it is acted on being a continuation of the rod, that by which it acts being perpendicular to the axis of the rod. The first set of teeth are dispersed/disposed so as to rest in a frame which has a slight motion round an axis; and each rod can be moved so that its teeth shall touch the frame above, on or below the axis. Those rods, then, which have their teeth on the axis do not receive motion from the frame, while the others receive motion in one direction or another, according as the teeth touch the frame above or below the axis. The perpendicular teeth at the other extremities may thus be made to move in either direction, or to remain stationery: and these last mentioned teeth act upon the rods which make up the frame of the product. This last frame precisely resembles the frame of the multiplicand, with the addition of the connecting part by which the multiplier acts upon it.
The process of multiplication is then as follows; the frame of the multiplier having been set, and also that of the multiplicand, the extremity of the multiplier frame is brought over the first rod of the multiplicand. To this extremity is attached a tooth which acts upon the rod of the multiplicand over which it comes, giving it a motion in one or the other direction, according as the slightly revolving frame of the multiplier is made to move in one or the other direction. The rule is, to move the revolving frame in such a way as to bring the rod of the multiplicand to its zero position; and this one motion multiplies the figure of the multiplicand by the whole of the multiplier, and by the action of the perpendicular teeth, exhibits the result upon the product frame. The lateral motion is then given to the whole of the multiplier apparatus, until the tooth comes upon the next figure rod of the multiplicand, and the revolving frame being then made to bring the new multiplicand rod to zero, the effect upon the product frame is that the new figure of the multiplicand is multiplied by the whole of the multiplier, and the result added to that of the preceding figure. This process is continued until the whole of the figures of the multiplicand are exhausted.
The result is then completely exhibited on the frame of the product, but not in its simplest form, For, whereas +1 or -1 should be the only digits in the final result, this intermediate result may exhibit +2 or -2, +3 or -3 etc on any rod. The carrying frame is a simple apparatus which, like the multiplier, has a lateral motion, and can be brought on any pair of consecutive rods. By one motion of the hand, it advances the left of two rods by a unit, and throws back the right hand rod by 3 units, or vice versa. Some little expertness is here necessary in making the carriages properly, with reference to the simplicity of the result: but there is no possibility of absolute error being introduced, since each process can only consist in altering a lower column by 3 units while the next column is altered in the contrary way by one unit.
The method of performing division is precisely the reverse of the preceding, and will hardly need description.
***
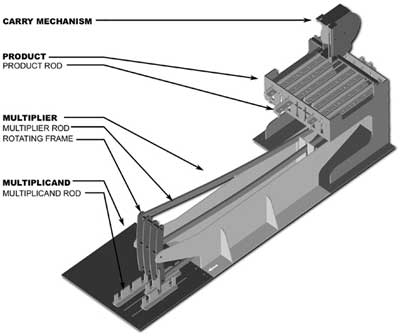
Almost all information, that can be found in the present-day for Fowler, has been discovered and classified by the researchers Pamela Vass and David Hogan, from North Devon, England. In 1999 they decided to contact a skillful mechanician — Mark Glusker, in order to make a replica of the machine. Due to the scarce historical information, Mr. Glusker had a hard time during his work but managed to produce a working device. The model was completed in about eight months and was presented to the Great Torrington Museum in a ceremony in August of 2000. Below you can see some sketches of the replica. All copyrights for the replica and photos are the property of Pamela Vass, David Hogan, and Mark Glusker.
The image featured at the top of this post is ©Unknown author / public domain

