James White

James White

Many thanks to Mr. Denis Roegel, Professor at Loria, France, for his seminal work on White’s adding machine

In 1822, James White (1762–1825), an English civil engineer and prolific inventor (see biography of James White), published a very interesting book—A New Century of Inventions: Being Designs and Descriptions of One Hundred Machines, Relating to Arts, Manufactures, and Domestic Life (the great Charles Babbage, the creator of Differential Engine and Analytical Engine was a subscriber of the book).

Late in his life (the preface mentions his declining health and approaching mortality), he decided to publish all (or at least the 100 implied in the title) of his inventions. Interestingly, between these 100 machines, described by White (some of original construction, some not), there is an adding machine, which seems to be the first key-driven calculator in the world.

It is unknown when exactly James White designed his advanced adding machine, but in any case it was long before the next known at the moment keyboard adders of Luigi Torchi (1834) and Jean-Baptiste Schwilgué (1844). Most probably the device has been designed in early 1800s, when White lived in Paris (he lived in France from the end of 1792 until February, 1815) and got acquainted with the machines of great French inventors like Pascaline of Blaise Pascal, automata of Vaucanson, and others.

In fact, Vaucanson was mentioned twice in the book, in connection of his chaîne Vaucanson, and it seems White planned to use it as the endless geering chain of his adding machine.

The Title Page of New Century of Inventions of James White

There is no doubt, that White was related and influenced by the British statesman and versatile scientist Charles Stanhope, who had a family seat in Chevening, Kent (he died there on 15 December 1816), where James White lived in early 1790s. Charles Mahon, 3rd Earl Stanhope, was the subject of several articles in this site, describing his mechanical calculating devices and logic machine). James White mentioned Stanhope three times in his book, as my noble Patron, and my noble friend. In the description of his adding machine, the paragraph, referring to Stanhope is:

I would just repeat, that I have not attempted here an arithmetical machine in general; but a Machine fit for the daily operations of the counting-house: by which to favour the thinking faculty, by easing it of this ungrateful and uncertain labour. Had I been thus minded, I could have gone further, in a road which has been already travelled by my noble friend the late Earl Stanhope, (then Lord Mahon) but I took a lower aim; intending in the words of Bacon—”to come home to men’s business and bosoms.”

The adding machine of White is a column adder with very interesting construction, which cannot be found in the later machines. The motion from the keys to the calculating mechanism and result dial is transferred by means of a pulley, that presses on an endless gearing chain. The chain is pushed out of its regular circular path by the depression of a key. This action causes the result wheel to turn an amount equal to the length of the key being pushed (the “1” key being 1 unit long, the “2” key, 2 units, etc).

Another interesting detail of the machine is a kind of floating point mechanism, in that the motion of wheel (see the figure 1 below) rotates the square shaft B G, on which lies a sliding wheel . This wheel can be moved to the appropriate position, should we add units, tens, hundreds, and so on, or other units (e.g. monetary, like pennies and farthings), such as those in use at the time of White.

As White didn’t patented his adding machine, and no account from his contemporaries survived for this device, we can assume that the machine does not appear to have been anything except a paper design and a working prototype has not been made.

Let’s see the White’s description of his adding machine (an excerpt of the book, pages 343–348, and plates 42 and 43):

AN ADDING MACHINE

Or Machine to Cast up large Columns of Figures.

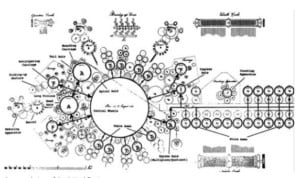
This Machine is not, generally, an arithmetical Machine. It points lower: and therefore promises more general utility. Though less comprehensive than machines which perform all the rules of arithmetic, it is thought capable of taking a prominent place in the counting-house, and there of effecting two useful purposes—to secure correctness; and thus, in many cases, to banish contention. It is represented in figs. 1, 2, 3, and 4 of Plate 42, and in figs. 3 and 4 of Plate 43.

There are two distinct classes of operations which may be noticed in this Machine: the one that does the addition, properly speaking; and the other that records it by figures, in the very terms of common arithmetic. The first operation is the adding: which is performed by means of an endless geering chain, stretched round the wheels A B C D, (fig. 1) and over the two rows of smaller pulleys a b c d e f g h i; where, observe, that the chain is bent round the pulley , merely to shorten the Machine, as otherwise the keys 1 2 3, &c. to 9, might have been placed in a straight line, and thus the bending of the chain have been avoided.

The chain, as before observed, geers in the wheels and , which both have ratchets to make them turn one way only. Now, the keys 1 2, &c. have pulleys at their lower ends, which press on the aforesaid chain more or less according to the number it is to produce, and the depth to which it is suffered to go by the bed on which the keys rest, when pressed down with the fingers. Thus, if the key 1 be pressed, as low as it can go, it will bend the chain enough to draw the wheel round one tooth—which the catch will secure, and which the wheel will permit it to do by the spring giving way.

But when the key 1 is suffered to rise again, this spring will tighten the chain by drawing it round the pulleys and , thus giving it a circulating motion, more or less rapid, according to the number of the key pressed. Thus, the key 5 would carry five teeth of the wheel to the left; and the catch would fix the wheel in this new position: after which the spring would tighten the chain in the same direction and manner as before. It is thus evident, that which-ever key is pressed down, a given number of teeth in the wheel , will be taken and secured by the catch ; and, afterwards, the chain be again stretched by the spring .

It may be remarked, that, in the figure, all the keys are supposed pressed down: so as to turn the wheel , a number of teeth equal to the sum of the digits 1, 2, 3—to 9. But this is merely supposed to shew the increasing defluxion of the chain, as the digits increase: for the fact can hardly ever occur. We draw from it, however, one piece of knowledge—which is, that should the eye, in computing, catch several numbers at once on the page, the fingers may impress them at once on the keys and chain; when the result will be the same as though performed in due succession.

Plate 42 of White’s New Century of Inventions

Thus then, the process of adding, is reduced to that of touching (and pressing as low as possible) a series of keys, which are marked with the names of the several digits, and each of which is sure to affect the result according to it’s real value: And this seems all that need be observed in the description of this process. It remains, however, to describe the 5th. figure, which is an elevation of the edge of the keyboard, intended to shew the manner in which the two rows of keys are combined and brought to a convenient distance, for the purpose of being easily fingered

We now come to the other part of the subject—that of recording the several effects before-mentioned. The principle feature in this part, is the System of carrying, or transferring to a new place of figures, the results obtained at any given one.

This operation depends on the effect we can produce by one wheel on another, placed near it, on the same pin; and on the possibility of affecting the second, much less than the first is affected: Thus, in fig. 3 and 4, (Plate 42,) if be any tooth of one such wheel, placed out of the plane of the pinion , it will, in turning, produce no effect upon that pinion: but if we drive a pin () into the tooth , that pin will move the pinion one tooth (and no more) every time this pin passes from to.

And if we now place a second wheel () similar to , at a small distance from it, so as to geer in all the teeth of the pinion , this latter wheel will be turned a space equal to one tooth, every time the pin passes the line of the centers of the wheel and pinion A B, (say from to .) It may be added, likewise, that this motion, of one tooth, is assured by the instrument shewn at E D, which is called in French a tout ou rien, (signifying all or nothing) and which, as soon as the given motion is half performed, is sure to effect the rest: and thus does this part of the process acquire, likewise, a great degree of certainty—if indeed, certainty admits of comparison.

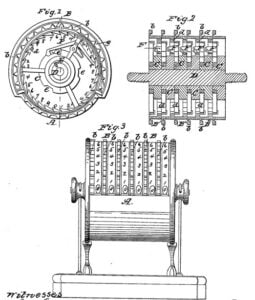
It is then, easy to perceive, how this effect on the different places of figures is produced; and it is clear, that with the chain motion just described, it forms the basis of the whole Machine. There is, however, one other process to be mentioned, and as the 2nd. figure is before us, we shall now advert to it. In adding up large sums, we have sometimes to work on the tens, sometimes on the hundreds; which mutations are thus performed: The wheel , (fig. 2) is the same as that , fig. 1; and it turns the square shaft B G, on which the wheels k l slide. The wheel is to our present purpose. It is now opposite the place of shillings; but by the slide , it can be successively placed opposite pounds, tens, hundreds, &c. at pleasure: on either of which columns, therefore, we can operate by the chain first described—the wheel being the common mover.

Plate 43 of White’s New Century of Inventions

We shall now turn to figs. 3 and 4 of Plate 43, which give another representation of the carrying-mechanism, adapted especially to the anomalous carriages of 4, 12, and 20, in reference to farthings, pence, shillings, and pounds, and then following the decuple ratio.

In fig. 3, k l represent the two acting wheels of the shaft B G, fig. 2; the latter dotted, as being placed behind the former; these wheels, however, are not our present object, but rather the carrying system before alluded to; and described separately, in fig. 3 of Plate 42. , in figures 3 and 4 (of Plate 43) is the first wheel of this series. It has 12 teeth with three carriage-pins (or plates) a, which jog the carrying pinion , at every passage of 4 teeth; thus shewing every penny that is accumulated by the farthings.

This is so, because the farthings are marked on the teeth of this first wheel in this order-1, 2, 3, 0; 1, 2, 3, &c. and it is in passing from 3 to 0, that this wheel, by the carriage-pinion , jogs forward the pence wheel C one tooth: But this pence wheel is divided into 12 numbers, from 0 to 11; and has on it only one carrying-pin (or plate) ; so that, here, there is no effect produced on the third wheel , until 12 pence have been brought to this second wheel , by the first, or farthing wheel.

Now, this third wheel , is marked, on it’s twenty teeth, with the figures 0 to 19, and makes, therefore, one revolution, then only, when there have been twenty shillings impressed upon it by twenty jogs of the carriage-pin , in the second wheel. But when this wheel has made one whole revolution, it’s single carriage-pin c, acting on the small carriage-pinion, like that c d, (but not shewn) jogs forward, by one tooth, the wheel, which expresses pounds; and having two carriage-pins e f, turns the wheel called tens of pounds, one tooth for every half turn of this wheel: and as, on all the succeeding wheels, to the left from –(see fig. 2, Plate 42) there are two sets of digits up to 10, and two carriage-pins; the decuple ratio now continues without any change: and thus can we cast up sums consisting of pounds, shillings, pence, and farthings, expressing the results, in a row of figures, exactly as they would be written by an accountant. The opening, through which they would appear, being shewn in fig. 1, at the point , corresponding with the line x y of fig. 2 in the same Plate.

I shall only remark, further, that the figures 3 and 4 in Plate 43, are of the natural size, founded, indeed, on the use of a chain that I think too large; being, in a word, the real chain de Vaucanson, mentioned in a former article: and that the figures of Plate 42 are made to half these dimensions, in order to bring them into a convenient compass on the Plate.

I would just repeat, that I have not attempted here an arithmetical machine in general; but a Machine fit for the daily operations of the counting-house: by which to favor the thinking faculty, by easing it of this ungrateful and uncertain labor. Had I been thus minded, I could have gone further, in a road which has been already travelled by my noble friend the late Earl Stanhope, (then Lord Mahon) but I took a lower aim; intending in the words of Bacon—”to come home to men’s business and bosoms.”

Next Up…

• Emory Seymour Ensign
• Gauss of Christel Hamann
• Dalton Adding Machine – Complete History of the Dalton Adding Machine

The image featured at the top of this post is ©G-Stock Studio/Shutterstock.com.