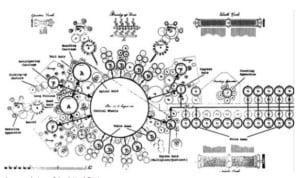
Invented by Leonardo Torres in 1920, the Torres calculating machine is a machine which solves essential addition, subtraction, multiplication, and division problems using a simple manner. It was a ground-breaking mechanical device which revolutionized the world of mathematics.
Torres’s machine was able to identify the roots of quadratic equations using both real and complex numbers, and was the first machine that was able to solve such equations. It calculates the numerical values of eight-degree polynomial roots and could produce both continuous and automated values.
Quick Facts
- Created
- 1910
- Creator
- Leonardo Torres y Quevedo
- Original Use
- Calculate polynomial roots
- Cost
- N/A
Torres’s calculating machine consisted of an arithmetic unit which was connected to a typewriter through which different commands could be typed and the results printed automatically.
About Leonardo Torres y Quevedo

Leonardo Torres y Quevedo (December 28, 1852 – December 18, 1936) was a late nineteenth- and early twentieth-century Spanish civil engineer and mathematician. Quevedo pioneered radio control and automated calculating machines, the chess automaton developer, and the designer of the three-lobed non-rigid Astra-Torres airship and Niagara Falls Whirlpool Aero Car. In addition, Torres-Quevedo invented wireless remote-control operation concepts with his Telekine. He was also a well-known Esperanto speaker.
On the Feast of the Holy Innocents, December 28, 1852, Leonardo Torres y Quevedo was born in a stone home in Santa Cruz de Igua, a little town near Molledo (Cantabria), Santander.
Luis Torres, his father, and Leonardo’s mother were clever and conservative individuals who attempted to dedicate as much time to their family despite traveling frequently. They also had a daughter, Joaquina Torres de Vildosola y Quevedo (born in 1851), and a younger son, Luis Torres Quevedo (born on March 21, 1855). Luis became a military officer and inventor with multiple patents to his credit (e.g., the photographic machine from 1886).
Leonardo Torres y Quevedo started his job with his father’s same railway business. Still, he quickly embarked on a long journey around Europe to learn firsthand about the scientific and technological developments of the day, particularly in the fledgling field of electricity. Upon his return to Spain, Torres settled in Santander. There Leonardo Torres y Quevedo self-funded his work and began a study and investigative routine that he never abandoned.
Leonardo Torres’s Calculating Machine: History
Torres Quevedo regularly traveled overseas, particularly to France, where he met top scientists. As a result, his work exhibited a high level of technical discipline, which was evident in the quality of his creations.
He submitted his “Report on Algebraic Machines” to the General Directorate of Public Works in Spain in 1893, and he also presented it in Paris later that year.
The algebraic machine of Torres was an analog computing device, featuring an mechanism based on cone-shaped pulley with a helical groove around it. The machine was used for the resolution of equations such as:
+ Ax = B
Torres Quevedo’s publications marked the beginning of a new era in mathematical theory based on novel ideas. His contributions resulted in the creation of cutting-edge new machinery. In addition, he created a succession of analog calculating devices to supplement his theoretical work, all mechanical.
Torres’s Calculating Machine: How it Worked

Leonardo Torres y Quevedo’s Calculating Machine could identify the roots of quadratic equations involving real and complex numbers since it was the first machine to solve equations; any quadratic problem might be solved using it.
As the variable increases or lowers, the gadget generates a succession of integer and rational values for which a polynomial function is continuously reevaluated.
This gadget calculates the numerical values of an eight-degree polynomial’s roots. Its development began in 1910 and ended in 1920, and its success is a testament to Torres-perseverance Quevedo’s ingenuity.
The device’s purpose was to produce continuous and automated values for a polynomial. Because the system is analog rather than digital, it can accept any value without making separate leaps.
It exhibits two significant advancements over previous work: the use of a logarithmic scale, which reduces the evaluation of monomial equations to additions, and the use of Torres-“husillos Quevedo’s sin fin” or unending spindles.
The wheels representing the unknown quantity spin around in a polynomial equation, and values of the sum of the variables are presented as a final result. The wheel of the unknown quantity reveals a root when this sum corresponds with the value of the second element.
Because of his theories on automation and devices, Torres Quevedo overcame the obstacles of building machines that performed calculations only using mechanical means. As a result, the calculating machine includes this automaton.
Later on Torres created a series of working prototypes of the above-mentioned machine. Possibly the first was a demonstration machine, capable of evaluating p x q–b. How successful this was in practice we do not know.
In 1920 Torres must have removed any uncertainty about his potential and knowledge to built a workable electromechanical calculating machine, because he startled the attendees at a Paris conference, marking the centenary of the invention of the first really practical calculating machine of Thomas Colmar, with a demonstration of his electromechanical arithmometer.
How to Use Torres’s Calculating Machine
This machine consisted of an arithmetic unit connected to a (possibly remote) typewriter, on which commands could be typed and the results printed automatically. Torres apparently had no thought of making such a machine commercially, viewing it instead as a means of demonstrating his ideas and techniques.
In order to use the system, the operator types at the typewriter, in the usual manner, the statement of the operation, which he wishes to have executed. Thus if he wants to multiply 532 by 257, he presses successively on the keys representing the digits 5, 3, 2, then on the space bar, on the key representing the multiplication sign, again on the space bar, and finally on the keys for the digits 2, 5, 7: the machine thus types the statement 532×257. That’s all!
The five drums D, D, D, D and D represent the dividend. The three cranks M, M and M represent the divisor. The three pointers Q, Q and Q represent the quotient. The operation of the machine is not automatically however.
In short, the operator knows that he must subtract the divisor (operate the crank ), if it is smaller than the remainder or move the carriage (operate the crank ), if it is larger; he will compare the two numbers after each operation to decide what the next action must be. When the operation is finished, he will press on the button to return to zero.
Leonardo Torres y Quevedo’s Calculating Machine: Historical Significance
Leonardo Torres y Quevedo created and successfully showed a chess-playing automaton in 1911 for the king and rook against the king endgame. This chess automaton was fully automated, with electrical sensors detecting the pieces on the board and a mechanical arm that moved the components independently. Torres exhibited a second chess automaton in 1920, which moved the pieces using magnets beneath the board.
Like many of his other inventions, the chess machines are still operating and in use. The gadget might be regarded as the world’s first computer game. When it was first shown in 1914 at the University of Paris, it sparked an interest. On November 6, 1915, it was first extensively reported in Scientific American as “Torres and His Remarkable Automatic Devices.”
Because of Torres Quevedo’s work on analog machines, the Paris Academy of Sciences welcomed his “Calculating Machines” report in 1900. As a result, he was elected to the Academy of Sciences in Madrid in 1901, where he delivered a lecture on algebraic machines.
The endless spindle was a critical component of the eight-term equation-solving computing machine. It created sums to answer the algorithm’s central equation. The mechanism was the first of its sort, and it was the most intriguing and unique of Torres Quevedo’s inventions.
Torres Quevedo’s calculating machine was both theoretically and practically groundbreaking. The endless spindle is a mechanical device that evaluates an expression’s logarithm as the sum of numerous logarithms, overcoming the difficulty of reaching enough precision with an automatic set of parts.
Next Up…
- The History of Next Differential Engines
- Christel Hamann’s Differential Engine Explained: Everything You Need To Know
- George Grant’s Difference Engine Explained — Everything You Need To Know
The image featured at the top of this post is ©Francisco González de Posada y Francisco A. González Redondo, CC BY 3.0.