Who was George Boole?
George Boole was a self-taught mathematician, philosopher, and logician. The majority of his professional life was spent as a mathematics professor at Queen’s College, Cork in Ireland. Boole worked in the fields of differential equations and algebraic logic.
He is best known for his book, The Laws of Thought, published in 1854. The Laws of Thought contains information on Boolean algebra. Boolean logic is known to have laid the foundation for the information age.
Quick Facts
- Full Name
- George Boole
- Net Worth
- Unknown
- Awards
- Gold Price in Mathematics & Keith Medal
- Children
- Mary, Margaret, Alicia, Lucy, and Ethel
- Nationality
- English
- Place of Birth
- England
- Fields of Expertise
- [“Mathematics”,”Logic”,”Philosophy”]
- Institutions
- Queen’s College, Cork (now University College Cork (UCC))
- Contributions
- Boolean Logic & Boolean Algebra (Symbolic Logic)
Early life
George Boole was born in Lincoln, Lincolnshire, England. His parents were John Boole senior and Mary Ann Joyce. Boole had a primary school education, and later, he was homeschooled by his father due to their decline in business. He has little formal and academic education, and was self-taught in modern languages.
At 16, Boole became a junior teacher at the Doncaster at Heigham’s School. This was when Boole became the financial supporter for his parents and younger siblings.
Boole also participated in the Lincoln Mechanics Institute, which was founded in 1933. It was then that Edward Bromhead helped George Boole with mathematics. Then, Rev. George Stevens Dickson of St Swithin’s, Lincoln gave Boole the calculus text of Sylvestre Francois Lacroix. Unfortunately, Boole didn’t have a proper teacher, and it took him many years to master calculus.
At 19, George Boole established his own school in Lincoln – Free School Lane. Four years later, following the death of Robert Hall, Boole took over Hall’s Academy in Waddington. In 1840, he moved back to Lincoln, where he ran a boarding school.
Boole was involved in the Lincoln Topographical society and served as a member of the committee. Boole became an influential local figure and admired John Kaye, an English churchman. Later, he joined the local campaign for early closing. It was formed to control the hours of labor in retail shops and to end Sunday trading. Starting in 1838, Boole networking with sympathetic British academic mathematicians and reading more widely. Also, Boole studied algebra in the form of symbolic methods and began to publish research papers.
Career
Professor at Cork
In 1849 Boole’s status as a mathematician was recognized when he was appointed as the first professor of mathematics at Queen’s College, Cork in Ireland.
What is George Boole known for?
George Boole is considered one of the founders of computer science and is known for his concept: Boolean logic. Boolean logic is a logical theory that acts as the basis of modern digital computers and other digital devices.
George Boole: Marriage, Divorce, Children, and Personal Life
Marriage
In 1855, Boole married Mary Everest, who later wrote several educational works on Boole’s principles. They met in 1850 while she was visiting her uncle, John Ryall, who was professor of Greek at Queen’s College, Cork in Ireland.
Children
Mary and George had 5 daughters: Mary, Margaret, Alicia, Lucy, and Ethel.
Tragedy
In November 1864, Boole walked three miles from his home to the university in heavy rainfall, then he lectured in wet clothes. Immediately, Boole became ill and developed pneumonia. Mary, his wife, believed she needed to wrap him in wet blankets to cure him. His condition worsened, and Boole died on December 8, 1864, due to fever-induced pleural effusion. Boole was buried in the Church of Ireland cemetery of St. Michael’s, Church Road, Blackrock. There is a commemorative plaque inside the adjoining church.

George Boole: Awards and Achievements
Royal Society Gold Prize in Mathematics
George Boole won the first gold prize for mathematics awarded by the Royal Society in 1844 for his paper “On a General Method in Analysis.”
Royal Society Keith Medal
He was awarded the Keith Medal by the Royal Society of Edinburgh in 1855.
Two years later, Boole was elected a Fellow of the Royal Society (FRS).
Boole received honorary degrees of LL.D. from the University of Dublin and the University of Oxford.
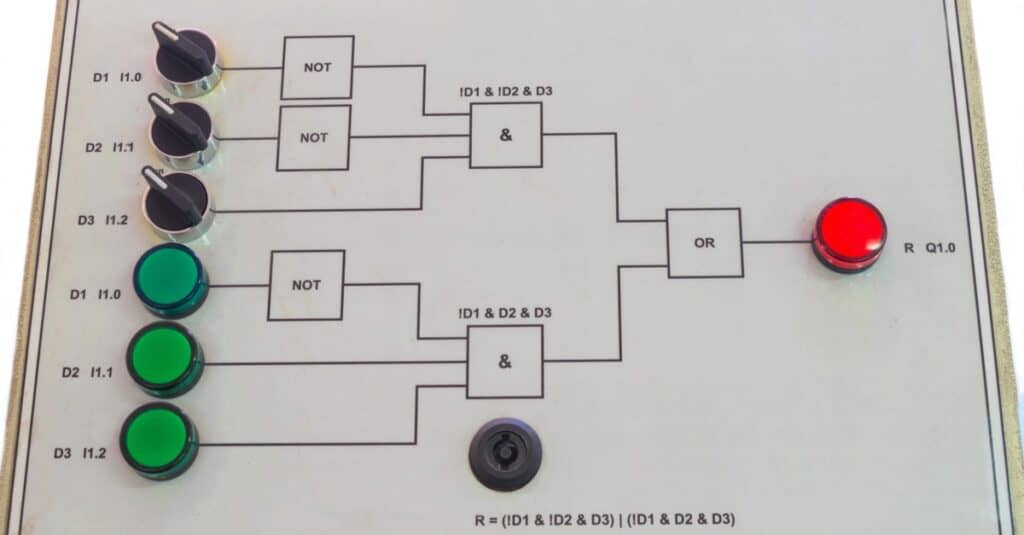
A training stand with sensors, switches, and a circuit of logic elements used in student training to illustrate Boolean logic. Boolean logic is a subsection of algebra that describes a set of simple rules and gates to help compare and manipulate logical statements.
George Boole’s Published Works and Books
The first paper that Boole published was “Researches in the Theory of Analytical Transformations, with a Special Application to the Reduction of the General Equation of the Second Order.” It was printed in the Cambridge Mathematical Journal in February 1840. This paper led to a friendship between Boole and the editor of the journal, Duncan Farquharson Gregory.
Boole published an influential paper in early invariant theory in 1841.
In 1844 he received a medal from the Royal Society for his memoir, “On a General Method in Analysis.” This was a contribution to the theory of linear differential equations, moving from the case of constant coefficients to variable coefficients. The innovation in operational methods is to admit that operations may not commute.
Boole published “The Mathematical Analysis of Logic” in 1847. This was his first work on symbolic logic.
Differential equations
In 1859 and 1860, Boole published two systematic treatises on mathematical subjects. First, “Treatise on Differential Equations” and then “Treatise on the Calculus of Finite Differences.”
Boole’s Identity
Boole published the treatise “On the Comparison of Transcendent, with Certain Applications to the Theory of Definite Integrals” in 1857. In the treatise, he studied the sum of residues of a rational function where he proved what we now call: Boole’s Identity – for any real numbers. There are generalizations of this identity that play an important role in the theory of the Hilbert transform.
Symbolic Logic
In 1847, Boole published a pamphlet titled “Mathematical Analysis of Logic,” later he wanted “An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities” to be seen as the mature statement of his views. It was believed that Boole disagreed with Aristotle’s logic; however, Boole only intended to systematize it. He wanted to provide it with a foundation and to extend its range of applicability. Boole initially became involved in logic during a debate on quantification between Sir William Hamilton and Augustus De Morgan.
This debate led to Boole founding what was first known as the “algebra of logic” tradition. Boole had many innovations of his principle of holistic reference, and it was later adopted by Gottlob Frege and other logicians who believed in the standard first-order logic.
In 2003 an article was published that provides a comparison and critical evaluation between Aristotelian logic and Boolean logic – it reveals the centrality of holistic reference in Boole’s philosophy of logic.
Probability theory
The second part of the “Laws of Thought” included an attempt to discover a general method in probabilities. “Boole’s goal was algorithmic: from the given probabilities of any system of events, to determine the consequent probability of any other even logical connected with those events.”
George Boole Quotes
“Of the many forms of false culture, a premature converse with abstractions is perhaps the most likely to prove fatal to the growth of a masculine vigour of intellect.”
“It is not of the essence of mathematics to be conversant with the ideas of number and quantity. Whether as a general habit of mind it would be desirable to apply symbolic processes to moral argument, is another question.”
“It is not of the essence of mathematics to be conversant with the ideas of number and quantity.”
“The general laws of Nature are not, for the most part, immediate objects of perception.”
“That language is an instrument of human reason, and not merely a medium for the expression of thought, is a truth generally admitted.”
“No matter how correct a mathematical theorem may appear to be, one ought never to be satisfied that there was not something imperfect about it until it also gives the impression of being beautiful.”
“I presume that few who have paid any attention to the history of the Mathematical Analysis, will doubt that it has been developed in a certain order, or that that order has been, to a great extent, necessary — being determined, either by steps of logical deduction, or by the successive introduction of new ideas and conceptions, when the time for their evolution had arrived.”
“Probability is expectation founded upon partial knowledge. A perfect acquaintance with all the circumstances affecting the occurrence of an event would change expectation into certainty, and leave nether room nor demand for a theory of probabilities.”
“It follows that the word probability, in its mathematical acceptance, has reference to the state of our knowledge of the circumstances under which an event may happen or fail. With the degree of information we possess concerning the circumstances of an event, the reason we have to think that it will occur, or, to use a single term, our expectation of it will vary. Probability is the expectation founded upon partial knowledge.”
“To unfold the secret laws and relations of those high faculties of thought by which all beyond the merely perceptive knowledge of the world and of ourselves is attained or matured, is a object which does not stand in need of commendation to a rational mind.”
“I am now about to set seriously to work upon preparing for the press an account of my theory of Logic and Probabilities which in its present state I look upon as the most valuable if not the only valuable contribution that I have made or am likely to make to Science and the thing by which I would desire if at all to be remembered hereafter.”
“I am fully assured, that no general method for the solution of questions in the theory of probabilities can be established which does not explicitly recognize, not only the special numerical bases of the science, but also those universal laws of thought which are the basis of all reasoning, and which, whatever they may be as to their essence, are at least mathematical as to their form.”
Up Next…
Let’s keep reading to dig into math theories and other principles that are important for computers!
- Logic Theorist Explained – Everything You Need To Know. We break down the first artificial intelligence programming.
- Here’s The Complete Guide to Boolean logic. Not enough information in this article on Boole’s concepts? Check this out.
- Here’s Your Complete Guide To Invariant Theory. More critical theories for artificial intelligence and machine learning.