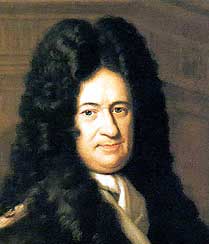
Key Points:

• Gottfried Wilhelm Freiherr Baron von Leibniz (1646-1716) invented the Stepped Reckoner.
• Leibniz helped invent the modern binary system, which uses symbols 0 and 1 for numbers and letters, being the first to introduce them in “Explanation of Binary Arithmetic” in 1703.
• Leibniz was the first mathematician to invent calculus, publishing on it in 1684, while Isaac Newton received the credit, publishing later in 1693.

Gottfried Wilhelm Leibniz

Gottfried Wilhelm Freiherr Baron von Leibniz (the inventor of the Stepped Reckoner and a dreamer for a thinking device) was born in Leipzig, Germany, on Sunday, 21 June 1646, (according to the Julian calendar) in the family of Friedrich Leibniz (1597-1652) and his third wife — Catharina Schmuck-Leibniz (1621-1664). Gottfried had a half-brother and a half-sister from the first marriage of his father, and a sister from the third, Anna Catharina (1648-1672).

The name of Leibniz might lead to the supposition, that the family was of Slavonic origin. His great-grandfather and grandfather held honorable offices under government, and his father, besides following the calling of a notary, was a professor of Moral Philosophy and Vice Chairman of the faculty of philosophy at the University of Leipzig. His mother, a daughter of a famous Leipzig lawyer, was carefully educated and smart woman, a pious Lutheran. This turned out to be very important for Gottfried, because no more than six years old, he had the misfortune to lose his father. Catharina devoted herself exclusively to the education of her children and exerted a great influence upon her son.

At a tender age, Gottfried was sent to the then highly popular Nikolaischule (Nicolai-school) (see the nearby photo) in Leipzig, where his extraordinary talent manifested itself in an insatiable desire for mental aliment. By 12, he had taught himself Latin, which he used freely all his life, and had begun studying Greek. At thirteen, he discovered one of his lifelong passions, the study of logic. He entered his father’s university at age 14, and completed university studies by 20, specializing in law and mastering the standard university courses in classics, logic, and scholastic philosophy. In 1666, he published his first book, also his habilitation thesis in philosophy, De Arte Combinatoria (On the Art of Combinations). When Leipzig declined to assure him a position teaching law upon graduation on account of his age, Leibniz submitted the thesis he had intended to submit at Leipzig to the University of Altdorf instead, and obtained his doctorate in law in five months. He then declined an offer of academic appointment at Altdorf, and accepted his first job, which he held only briefly, as secretary to a society of alchemists at Nuremberg. At the time, he was keenly interested in alchemy, and he believed that the newly discovered phosphorus might hold the key to the philosophers’ stone. In later life however, he came to believe that alchemy was mere superstition, and he seems to have destroyed most of his papers relating to alchemy.

However, Leibniz disliked the stuffiness and pettiness of academia and sought a diplomatic career. One of the most important diplomats of the time, Johann Christian von Boyneburg (1622-1672), took him under his wing and secured a post for him at the court of the archbishop of Mainz, the Prince Elector Johann Philipp von Schönborn. The rest of his life, Leibniz was in the service of the Elector of Mainz, and then to the Duke Johann Friedrich of Brunswick-Lüneburg and his successors in Hanover.

As a advisor of the Elector of Mainz, Leibniz published an essay, in which proposed to protect the exhausted from the Thirty Years’ War German-speaking Europe, by distracting Louis XIV attention to the conquest of Egypt and India. In 1672 the French government invited Leibniz to Paris for discussion. Nothing came of the plan, but Leibniz spent the four most instructive and constructive years of his life in Paris. Paris was then the centre of philosophical activity in Europe, and Leibniz made a wide range of acquaintances, including the philosophers Arnauld and Malebranche, mathematician Christian Huygens and the physicist Edme Mariotte. Under the tutorship of Huygens, he made such rapid strides in mathematics, that by the end of his stay, he had already developed what was to be one of the greatest mathematical discoveries of all time, namely the infinitesimal calculus. (In fact Newton probably got there first, but with an inferior notation. The one we use now is Leibniz’s. The much later dispute as to who was first was a major factor in bringing about the long-lasting divide between Continental and British philosophy and science.) He managed to get access to the unpublished writings of the two greatest philosophers of the previous generation, Pascal and Descartes, and some of the latter survive only through copies he made.

In 1672 Leibniz became acquainted with the calculating machine of Pascal , which he decided to improve. In the beginning of 1673, Leibniz was sent to London, where he met some english scientists, presented his treatise called The Theory of Concrete Motion and demonstrated the prototype of his calculating machine to the Royal Society. The Society made him an external member.

While in Paris, Leibniz also not only worked on physics and mathematics, and designed a calculating machine, but in addition, he wrote about a number of technological ideas, such as an improved system of balance wheels for watches, a submarine, and an aneroid barometer, definition of a ship’s geographical position without a compass, a plan of an underwater vessel and a kind of a tank propelled by gunpowder. Leibniz considered also the possibilities of space flights but rejected the plan due to thinness of air. In 1679, while mulling over his binary arithmetic, Leibniz imagined a machine in which binary numbers were represented by marbles, governed by a rudimentary sort of punched cards, a dream for binary universal computer.

In 1676 Leibniz was promoted to Privy Counsellor of Justice to the Duke of Hanover, and to the rest of his life he served three consecutive rulers of the House of Brunswick in Hanover as historian, political adviser, and as librarian of the ducal library. The Duke was sympathetic towards Leibniz’s many diverse plans and let him conduct a large correspondence with some of the most distinguished learned men of his time. The court of Hanover was the cultural centre of North-Germany at the time.

Among other duties, Leibniz was busy with chemistry and technical applications. He was assigned to improve the output of the mines of Harz by developing the power transmission and pump technique. After this Leibniz was assigned to write the history of the Guelfs (the ruling dynasty of Hanover) in 1685. The project turned out to grow to such vast measurements, that to complete the project it would require a whole academy instead of one man.

Later on Leibniz performed several diplomatic and scientific missions and wrote two philosophical treatises.

He is considered as the most important logician between Aristotle and 1847, when George Boole and Augustus De Morgan each published books that began modern formal logic. Leibniz enunciated the principal properties of what we now call conjunction, disjunction, negation, identity, set inclusion, and the empty set.

Leibniz made also important discoveries in the fields of mathematics, physicists, geology, life sciences and palaeontology, psychology and sociology. He established the German Academy of Sciences; formulated an enormously influential philosophy which held that the universe was made out of irreducible, ever-changing substances called monads; sought the reunification of the Catholic and Protestant churches; founded the science of topology; was appointed an advisor to the Holy Roman Emperor and made a baronet. That’s possibly the reason, some people to call him the last universal mind of the mankind

Leibniz died on the 14th of November, 1716, his closing years enfeebled by disease, harassed by controversy, embittered by neglect; but to the last he preserved the indomitable energy and power of work to which is largely due the position he holds as, more perhaps than any one in modern times, a man of almost universal attainments and almost universal genius. At Hanover, Eckhart, his secretary, was his only mourner; “he was buried”, says an eyewitness, “more like a robber than what he really was, the ornament of his country.”

The image featured at the top of this post is ©Unknown author / public domain.