Anton Braun
The German mechanic, constructor and optician Anton (Antonius) Braun (see biography of Anton Braun) (1686-1728) from Möhringen (Baden-Württemberg, Germany), was appointed in 1724 as a mechanician and optician of the imperial court in Vienna, Austria. In the same 1724 he started to design a calculating machine for the purposes of the court.
He finished his work in 1727, producing a calculating machine of a very good design and workmanship. When in 1727 he presented the machine to the Holy Roman Emperor Karl VI, he got into favour of the Emperor and was appointed as imperial instrument maker, and was granted with diamond chain, occupied with the portrait of the Emperor and a huge sum of money—10000 guilders.
The machine of Anton Braun is quite big—a finely decorated and looking like a renaissance table clock cylinder, made of steel, silver and brass with almost 40 cm diameter and 21 cm height.

The calculating machine of Anton Braun (© Deutsches Museum, Munich)
The calculating mechanism was based on the pin-wheel (or sprocket wheel), invented by Leibniz and Poleni, and described by Leupold. Obviously Braun was acquainted with the encyclopedia Theatrum Arithmetico–Geometricum of Leupold, where was described the machine of Poleni.
But in contrast to the machine of Poleni, the Braun’s was a smaller, more easy for use and perfectly manufactured device, which actually is considered as the first easy to operate mechanical calculating machine.
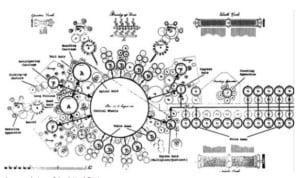
The machine’s six-place setting mechanism is under the form of six circular segments arranged in a circle on the top, with nine levers each (for digits 1 to 9), which move the relevant pins radially outwards on the pin-wheels below.
Turning the crank adds the entered number to the result mechanism (12-place with complementary numbers shown), and the result is shown in the windows along the periphery of the cover (the silver-plated part). The setting mechanism can be rotated with respect to the result mechanism so that both multiplication and division are possible. The machine also featured a single-digit revolution counter.

The first calculating machine of Anton Braun from 1727 (© Technischen Museum, Wien)

There is another calculating machine of Braun, still preserved in Technischen Museum in Wien (see the upper images), which had an engraved dedication to the Kaiser Karl VI and also the self-conscious signature “Antonius Braun S.C.M. Opticus et mathematicus”, with the year of completion in 1727. There is information however, that this machine is not the original one, made by Anton Braun in 1720s, but a copy, made in 1766 by his son—Anton Braun the Younger (1708-1776), who just like his father was a skilful optician and watchmaker.
It seems Anton Braun actually designed two quite different internally calculating machines. Besides the device, presented to the Emperor, he designed also another much smaller calculating machine, similar in appearance to the first, but its calculating mechanism is almost identical to the Leupold’s machine and it is based on a ratchet-wheel.
This machine probably was only begun in the workshop of Braun, but after his death (he died on 20 April 1728 from an infection of the lungs) it was finished as late as in 1736 by his son and by the famous French mechanician Phillippe Vayringe (1684-1746), who was hired by the Emperor to fix the machine, kept in his collection. The machine (on its lid is engraved Braun invenit, Vayringae fecit) (Invented by Braun, manufactured by Vayringe) is now in the exposition of Deutsches Museum, Munich (see the first photo of the article and the photos below).

The calculating machine of Leupold-Braun-Vayringe from 1736 (© Deutsches Museum, Munich)

The machine featured a single central so-called adapting segment, which allowed the number of special, complicated parts to be greatly reduced. Below the setting mechanism was placed a set of vertical cylinders, each with nine rods of different lengths rising from its top. For example, if the digit nine was entered, the shortest rod was rotated to the outside, as then one full turn of the crank turned the central adapting segment once around the central axle.
It consisted of a disc with various steps as well as a segment with nine cogs. When it was turned once round, it passed the setting cylinders, on each of which a certain rod pushed the corresponding step outwards, whereupon the cog-segment of the adapting segment engaged a cog-wheel of the result mechanism and thus rotated the numbered disc to the correct digit in the corresponding window.
Thus, the smaller the entered digit was, the later the adapting segment engaged and fewer cogs were moved. Multiplication was done by repeated revolutions of the crank, as a place-shift mechanism enables multiplying with multi-digit multipliers. Subtraction (and division) were done using the 9-complements of digits.
Even though the tens-carry mechanism of the machine did not function properly in every place, the idea of a central adapting segment was a great innovation which found extensive use in several brilliant machines some 200 years later on, like the magnificent Curta of Herzstark, even though it used a stepped drum as the central element.
The machine is commonly named Leupold-Braun-Vayringe machine, due to the fact, that the idea of the calculating mechanism was proposed by Leupold, the construction was made by Braun, while the actual manufacturing was made by Vayringe.

A copy of the calculating machine of Braun-Vayringe from 1736 with a glass lid
There are also several modern replicas of the machine, one of them is very beautiful with its transparent glass lid (see the upper photo).
The image featured at the top of this post is ©U.Name.Me, CC BY-SA 4.0, via Wikimedia Commons.