The article written by Percy E. Ludgate in 1909 first gives thanks to Professor C. V. Boys, F.R.S. for his assistance on the subject of analytical machines. Ludgate also refers to the work of Charles Babbage who had previously invented two Difference Engines and then and Analytical Machine. However, Babbage died before his machine was completed and his work was then continued by his son, Henry. In this text, Ludgate goes on to describe his knowledge of Babbage’s Analytical Machine and how his own machine resembles it.
Analytical machines must have some way of storing the data relating to the problem that needs to be solved, and Ludgate goes on to explain in detail how he has achieved this with his own design. He thoroughly explains his methods and his results in a paper which showcases his expansive knowledge of the subject.
ON A PROPOSED ANALYTICAL MACHINE
by Percy E. Ludgate
Read February 23. Ordered for Publication March 9. Published April 28, 1909
I purpose to give in this paper a short account of the result of about six years’ work, undertaken by me with the object of designing machinery capable of performing calculations, however intricate or laborious, without the immediate guidance of the human intellect.
In the first place I desire to record my indebtedness to Professor C. V. Boys, F.R.S., for the assistance which I owe to his kindness in entering into correspondence with me on the matter to which this paper is devoted.
It would be difficult and very inadvisable to write on the present subject without referring to the remarkable work of Charles Babbage, who, having first invented two Difference Engines, subsequently (about eighty years ago) designed an Analytical Engine, which was shown to be at least a theoretical possibility; but unfortunately its construction had not proceeded far when its inventor died.
Since Babbage’s time hisseems to have been almost forgotten; and it is probable that no living person understands the details of its projected mechanism. My own knowledge of Babbage’s Engines is slight, and for the most part limited to that of their mathematical principles.
The following definitions of an Analytical Engine, written by Babbage’s contemporaries, describe its essential functions as viewed from different standpoints:
‘A machine to give us the same control over the executive which we have hitherto only possessed over the legislative department of mathematics.’*
*Q Babbage: ‘Passages from the Life of a Philosopher’, p. 129.
‘The material expression of any indefinite function of any degree of generality and complexity, such as, for instance: , , , log , sin , &c.), which is, it will be observed, a function of all other possible functions of any number of quantities.’†
†R. Taylor’s ‘Scientific Memoirs’, 1843, vol. iii., p. 691.
‘An embodying of the science of operations constructed with peculiar reference to abstract number as the subject of those operations.’*
*loc. cit., p. 694.
‘A machine for weaving algebraical patterns.’†
†loc. cit., p. 696.
These four statements show clearly that an Analytical Machine ‘does not occupy common ground with mere “calculating machines”. It holds a position wholly its own’.
In order to prevent misconception, I must state that my work was not based on Babbage’s results—indeed, until after the completion of the first design of my machine, I had no knowledge of his prior efforts in the same direction. On the other hand, I have since been greatly assisted in the more advanced stages of the problem by, and have received valuable suggestions from, the writings of that accomplished scholar.
There is in some respects a great resemblance between Babbage’s Analytical Engine and the machine which I have designed—a resemblance which is not, in my opinion, due wholly to chance, but in a great measure to the nature of the investigations, which tend to lead to those conclusions on which the resemblance depends. This resemblance is almost entirely confined to the more general, abstract, or mathematical side of the question; while the contrast between the proposed structure of the two projected machines could scarcely be more marked.
It is unnecessary for me to prove the possibility of designing a machine capable of automatically solving all problems which can be solved by numbers. The principles on which an Analytical Machine may rest ‘have been examined, admitted, recorded, and demonstrated’.‡ I would refer those who desire information thereon to the Countess of Lovelace’s translation of an article on Babbage’s Engine, which, together with copious notes by the translator, appears in R. Taylor’s ‘Scientific Memoirs’, vol. iii.; to Babbage’s own work, ‘Passages from the Life of a Philosopher’; and to the Report of the British Association for the year 1878, p. 92. These papers furnish a complete demonstration that the whole of the developments and operations of analysis are capable of being executed by machinery.
‡C. Babbage: ‘Passages from the Life of a Philosopher’, p. 450.
Notwithstanding the complete and masterly treatment of the question to be found in the papers mentioned, it will be necessary for me briefly to outline the principles on which an Analytical Machine is based, in order that my subsequent remarks may be understood.
An Analytical Machine must have some means of storing the numerical data of the problem to be solved, and the figures produced at each successive step of the work (together with the proper algebraical signs); and, lastly, a means of recording the result or results. It must be capable of submitting any two of the numbers stored to the arithmetical operation of addition, subtraction, multiplication, or division.
It must also be able to select from the numbers it contains the proper numbers to be operated on; to determine the nature of the operation to which they are to be submitted; and to dispose of the result of the operation, so that such result can be recalled by the machine and further operated on, should the terms of the problem require it.
The sequence of operations, the numbers (considered as abstract quantities only) submitted to those operations, and the disposition of the result of each operation, depend upon the algebraical statement of the calculation on which the machine is engaged; while the magnitude of the numbers involved in the work varies with the numerical data of that particular case of the general formula which is in process of solution.
The question therefore naturally arises as to how a machine can be made to follow a particular law of development as expressed by an algebraic formula. An eminently satisfactory answer to that question (and one utilized by both Babbage and myself) is suggested by the Jacquard loom, in which interesting invention a system of perforated cards is used to direct the movements of the warp and weft threads, so as to produce in the woven material the pattern intended by the designer.
It is not difficult to imagine that a similar arrangement of cards could be used in a mathematical machine to direct the weaving of numbers, as it were, into algebraic patterns, in which case the cards in question would constitute a kind of mathematical notation. It must be distinctly understood that, if a set of such cards were once prepared in accordance with a specified formula, it would possess all the generality of algebra, and include an infinite number of particular cases.
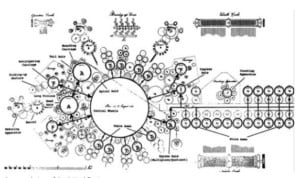
I have prepared many drawings of the machine and its parts; but it is not possible in a short paper to go into any detail as to the mechanism by means of which elaborate formulae can be evaluated, as the subject is necessarily extensive and somewhat complicated; and I must, therefore, confine myself to a superficial description, touching only points of particular interest or importance.
Babbage’s Jacquard-system and mine differ considerably; for, while Babbage designed two sets of cards—one set to govern the operations, and the other set to select the numbers to be operated on—I use one sheet or roll of perforated paper (which, in principle, exactly corresponds to a set of Jacquard- cards) to perform both these functions in the order and manner necessary to solve the formula to which the particular paper is assigned.
To such a paper I apply the term formula-paper. Each row of perforations across the formula-paper directs the machine in some definite step in the process of calculation—such as, for instance, a complete multiplication, including the selection of the numbers to be multiplied together. Of course a single formula-paper can be used for an indefinite number of calculations, provided that they are all of one type or kind (i.e. algebraically identical).
In referring to the numbers stored in the machine, the difficulty arises as to whether we refer to them as mere numbers in the restricted arithmetical sense, or as quantities, which, though always expressed in numerals, are capable of practically infinite variation. In the latter case they may be regarded as true mathematical variables. It was Babbage’s custom (and one which I shall adopt) when referring to them in this sense to use the term ‘Variable’ (spelt with capital V), while applying the usual meanings to the words ‘number’ and ‘variable’.
In my machine each Variable is stored in a separate shuttle, the individual figures of the Variable being represented by the relative positions of protruding metal rods or ‘type’, which each shuttle carries. There is one of these rods for every figure of the Variable, and one to indicate the sign of the Variable. Each rod protrudes a distance of from 1 to 10 units, according to the figure or sign which it is at the time representing.
The shuttles are stored in two co-axial cylindrical shuttle-boxes, which are divided for the purpose into compartments parallel to their axis. The present design of the machine provides for the storage of 192 Variables of twenty figures each; but both the number of Variables and the number of figures in each Variable may, if desired, be greatly increased. It may be observed, too, that the shuttles are quite independent of the machine, so that new shuttles, representing new Variables, can be introduced at any time.
When two Variables are to be multiplied together, the corresponding shuttles are brought to a certain system of slides called the index, by means of which the machine computes the product. It is impossible precisely to describe the mechanism of the index without drawings; but it may be compared to a slide-rule on which the ‘usual markings are replaced by moveable blades. The index is arranged so as to give several readings simultaneously. The numerical values of the readings are indicated by periodic displacements of the blades mentioned, the duration of which displacements are recorded in units measured by the driving shaft on a train of wheels called the mill, which performs the carrying of tens, and indicates the final product.
The product can be transferred from thence to any shuttle, or to two shuttles simultaneously, provided that they do not belong to the same shuttle-box. The act of inscribing a new value in a shuttle automatically cancels any previous value that the shuttle may have contained. The fundamental action of the machine may be said to be the multiplying together of the numbers contained in any two shuttles, and the inscribing of the product in one or two shuttles. It may be mentioned here that the fundamental process of Babbage’s Engine was not multiplication but addition.
Though the index is analogous to the slide-rule, it is not divided logarithmically, but in accordance with certain index numbers, which, after some difficulty, I have arranged for the purpose. I originally intended to use the logarithmic method, but found that some of the resulting intervals were too large; while the fact that a logarithm of zero does not exist is, for my purpose, an additional disadvantage. The index numbers (which I believe to be the smallest whole numbers that will give the required results) are contained in the following tables:
Column 1 of Table 1 contains zero and the nine digits, and column 2 of the same Table the corresponding simple index numbers. Column 1 of Table 2 sets forth all partial products (a term applied to the product of any two units), while column 2 contains the corresponding compound index numbers. The relation between the index numbers is such that the sum of the simple index numbers of any two units is equal to the compound index number of their product. Table 3 is really a re-arrangement of Table 2, the numbers 0 to 66 (representing 67 divisions on the index) being placed in column 1, and in column 2, opposite to each number in column 1 which is a compound index number, is placed the corresponding simple product.
| Table 1
| ||||||
|---|---|---|---|---|---|---|
| UNIT | SIMPLE INDEX NO. | ORDINAL | ||||
| 50 | ||||||
| 23 | ||||||
| 33 | ||||||
| 14 |
| Table 2
| |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PARTIAL PRODUCT | COMP INDEX NO. | PARTIAL PRODUCT | COMP INDEX NO. | PARTIAL PRODUCT | COMP INDEX NO. | ||||||
| 15 | 30 | 36 | 16 | ||||||||
| 16 | 40 | 26 | |||||||||
| 18 | 15 | 42 | 41 | ||||||||
| 20 | 25 | 45 | 37 | ||||||||
| 23 | 21 | 40 | 48 | 11 | |||||||
| 24 | 10 | 49 | 66 | ||||||||
| 33 | 25 | 46 | 54 | 22 | |||||||
| 27 | 21 | 56 | 36 | ||||||||
| 14 | 28 | 35 | 63 | 47 | |||||||
| 10 | 24 | 30 | 31 | 64 | |||||||
| 12 | 32 | 72 | 17 | ||||||||
| 14 | 34 | 35 | 56 | 81 | 28 | ||||||
| Comp. index numbers of zero: 50, 51, 52, 53, 57, 58, 64, 73, 83, 100 |
| Table 3
| |||||||
|---|---|---|---|---|---|---|---|
| COMP INDEX NO. | PARTIAL PRODUCT | COMP INDEX NO. | PARTIAL PRODUCT | ||||
| 34 | 14 | ||||||
| 35 | 28 | ||||||
| 36 | 56 | ||||||
| 37 | 45 | ||||||
| 16 | 38 | ||||||
| 32 | 39 | ||||||
| 64 | 40 | 21 | |||||
| 41 | 42 | ||||||
| 42 | |||||||
| 12 | 43 | ||||||
| 10 | 24 | 44 | |||||
| 11 | 48 | 45 | |||||
| 12 | 46 | 25 | |||||
| 13 | 47 | 63 | |||||
| 14 | 48 | ||||||
| 15 | 18 | 49 | |||||
| 16 | 36 | 50 | |||||
| 17 | 72 | 51 | |||||
| 18 | 52 | ||||||
| 19 | 53 | ||||||
| 20 | 54 | ||||||
| 21 | 27 | 55 | |||||
| 22 | 54 | 56 | 35 | ||||
| 23 | 57 | ||||||
| 24 | 10 | 58 | |||||
| 25 | 20 | 59 | |||||
| 26 | 40 | 60 | |||||
| 27 | 61 | ||||||
| 28 | 81 | 62 | |||||
| 29 | 63 | ||||||
| 30 | 15 | 64 | |||||
| 31 | 30 | 65 | |||||
| 32 | 66 | 49 | |||||
| 33 |
Now, to take a very simple example, suppose the machine is supplied with a formula-paper designed to cause it to evaluate for given values of , , , and , in the equation ab + cd = x and suppose we wish to find the value of in the particular case where = 9247, = 8132, = 21893, and = 823.
The four given numbers are first transferred to the machine by the key-board hereafter mentioned; and the formula-paper causes them to be inscribed in four shuttles. As the shuttles of the inner and outer co-axial shuttle-boxes are numbered consecutively, we may suppose the given values of and to be inscribed in the first and second shuttles respectively of the inner box, and of and in the first and second shuttles respectively of the outer box; but it is important to remember that it is a function of the formula-paper to select the shuttles to receive the Variables, as well as the shuttles to be operated on, so that (except under certain special circumstances, which arise only in more complicated formulae) any given formula-paper always selects the same shuttles in the same sequence and manner, whatever be the values of the Variables. The magnitude of a Variable only effects the type carried by its shuttle, and in no way influences the movements of the shuttle as a whole.
The machine, guided by the formula-paper, now causes the shuttle-boxes to rotate until the first shuttles of both inner and outer boxes come opposite to a shuttle-race. The two shuttles are then drawn along the race to a position near the index; and certain slides are released, which move forward until stopped by striking the type carried by the outer shuttle.
The slides in question will then have moved distances corresponding to the simple index numbers of the corresponding digits of the Variables . In the particular case under consideration, the first four slides will therefore move 3, 0, 7, and 1 units respectively, the remainder of the slides indicating zero by moving 50 units (see Table 1).
Another slide moves in the opposite direction until stopped by the first type of the inner shuttle, making a movement proportional to the simple index number of the first digit of the multiplier —in this case 14. As the index is attached to the last-mentioned slide, and partakes of its motion, the relative displacements of the index and each of the four slides are respectively 3 + 14, 0 + 14, 7 + 14, and 1 + 14 units (that is, 17, 14, 21, and 15 units), so that pointers attached to the four slides, which normally point to zero on the index, will now point respectively to the 17th, 14th, 21st and 15th divisions of the index. Consulting Table 3, we find that these divisions correspond to the partial products 72, 9, 27, and 18. In the index the partial products are expressed mechanically by movable blades placed at the intervals shown in column 2 of the third table.
Now, the duration of the first movement of any blade is as the unit figure of the partial product which it represents, so that the movements of the blades concerned in the present case will be as the numbers 2, 9, 7, and 8, which movements are conveyed by the pointers to the mill, causing it to register the number 2978. A carriage near the index now moves one step to effect multiplication by 10, and then the blades partake of a second movement, this time transferring the tens’ figures of the partial products (i.e. 7, 0, 2, and 1) to the mill, which completes the addition of the units’ and tens’ figures thus:
the result being the product of the multiplicand by the first digit of the multiplier . After this the index makes a rapid reciprocating movement, bringing its slide into contact with the second type of the inner shuttle (which represents the figure 2 in the quantity ), and the process just described is repeated for this and the subsequent figures of the multiplier a until the whole product ab is found. The shuttles are afterwards replaced in the shuttle-boxes, the latter being then rotated until the second shuttles of both boxes are opposite to the shuttle-race.
These shuttles are brought to the index, as in the former case, and the product of their Variables (21893 x 823) is obtained, which, being added to the previous product (that product having been purposely retained in the mill), gives the required value of . It may be mentioned that the position of the decimal point in a product is determined by special mechanism which is independent of both mill and index. Most of the movements mentioned above, as well as many others, are derived from a set of cams placed on a common shaft parallel to the driving-shaft; and all movements so derived are under the control of the formula-paper.
The ordinals in Table 1 are not mathematically important, but refer to special mechanism which cannot be described in this paper, and are included in the tables merely to render them complete.
The sum of two products is obtained by retaining the first product in the mill until the second product is found—the mill will then indicate their sum. By reversing the direction of rotation of the mill before the second product is obtained, the difference of the products results. Consequently, by making the multiplier unity in each case, simple addition and subtraction may be performed.
In designing a calculating machine it is a matter of peculiar difficulty and of great importance to provide for the expeditious carrying of tens. In most machines the carryings are performed in rapid succession; but Babbage invented an apparatus (of which I have been unable to ascertain the details) by means of which the machine could ‘foresee’ the carryings and act on the foresight. After several years’ work on the problem, I have devised a method in which the carrying is practically in complete mechanical independence of the adding process, so that the two movements proceed simultaneously. By my method the sum of numbers of figures would take 9 + units of time.
In finding the product of two numbers of twenty figures each, forty additions are required (the units’ and tens’ figures of the partial products being added separately). Substituting the values 40 and 20 for and , we get 9 x 40 + 20 = 380, or 9½ time-units for each addition—the time-unit being the period required to move a figure-wheel through 1/10 revolution.
With Variables of 20 figures each the quantity n has a constant value of 20, which is the number of units of time required by the machine to execute any carrying which has not been performed at the conclusion of an indefinite number of additions. Now, if the carryings were performed in succession, the time required could not be less than 9 + , or 29 units for each addition, and is, in practice, considerably greater.*
*For further notes on the problem of the carrying of tens, see C. Babbage: ‘Passages from the Life of a Philosopher’, p. 114, etc.
In ordinary calculating machines division is accomplished by repeated subtractions of the divisor from the dividend. The divisor is subtracted from the figures of the dividend representing the higher powers of ten until the remainder is less than the divisor. The divisor is then moved one place to the right, and the subtraction proceeds as before. The number of subtractions performed in each case denotes the corresponding figure of the quotient.
This is a very simple and convenient method for ordinary calculating machines; but it scarcely meets the requirements of an Analytical Machine. At the same time, it must be observed that Babbage used this method, but found it gave rise to many mechanical complications.
My method of dividing is based on quite different principles, and to explain it I must assume that the machine can multiply, add, or subtract any of its Variables; or, in other words, that a formula-paper can be prepared which could direct the machine to evaluate any specified function (which does not contain the sign of division or its equivalent) for given values of its variables.
Suppose, then, we wish to find the value of p/q for particular values of and which have been communicated to the machine. Let the first three figures of be represented by f, and let be the reciprocal of , where is expressed as a decimal of 20 figures. Multiplying the numerator and denominator of the fraction by , we have (Ap)/(Aq), where Aq must give a number of the form l00… because Aq = . On placing the decimal point after the unit, we have unity plus a small decimal. Represent this decimal by : then
| Ap 1 + | or | Ap(1 + -1 |
Expanding by the binomial theorem
| (1) | Ap(1 – + – + – + etc.), |
or
| (2) | Ap(1 – )(1 + )(1 + )(l + ),etc. |
The series (1) converges rapidly, and by finding the sum as far as 10 we obtain the correct result to at least twenty figures; whilst the expression (2) gives the result correctly to at least thirty figures. The position of the decimal point in the quotient is determined independently of these formulae. As the quantity must be the reciprocal of one of the numbers 100 to 999, it has 900 possible values.
The machine must, therefore, have the power of selecting the proper value for the quantity , and of applying that value in accordance with the formula. For this purpose the 900 values of are stored in a cylinder—the individual figures being indicated by holes of from one to nine units deep in its periphery. When division is to be performed, this cylinder is rotated, by a simple device, until the number A (represented on the cylinder by a row of holes), which is the reciprocal of the first three figures of the divisor, comes opposite to a set of rods.
These rods then transfer that number to the proper shuttle, whence it becomes an ordinary Variable, and is used in accordance with the formula. It is not necessary that every time the process of division is required the dividing formula should be worked out in detail in the formula-paper. To obviate the necessity of so doing the machine is provided with a special permanent dividing cylinder, on which this formula is represented in the proper notation of perforations.
When the arrangement of perforations on the formula-paper indicates that division is to be performed, and the Variables which are to constitute divisor and dividend, the formula-paper then allows the dividing cylinder to usurp its functions until that cylinder has caused the machine to complete the division.
It will be observed that, in order to carry out the process of division, the machine is provided with a small table of numbers (the numbers ) which it is able to consult and apply in the proper way. I have extended this system to the logarithmic series, in order to give to that series a considerable convergency; and I have also introduced a logarithmic cylinder which has the power of working out the logarithmic formula, just as the dividing cylinder directs the dividing process. This system of auxiliary cylinders and tables for special formulae may be indefinitely extended.
The machine prints all results, and, if required, the data, and any noteworthy values which may transpire during the calculation. It may be mentioned, too, that the machine may be caused to calculate and print, quite automatically, a table of values—such, for instance, as a table of logs, sines, squares, etc. It has also the power of recording its results by a system of perforations on a sheet of paper, so that when such a number-paper (as it may be called) is replaced in the machine, the latter can ‘read’ the numbers indicated thereon, and inscribe them in the shuttles reserved for the purpose.
Among other powers with which the machine is endowed is that of changing from one formula to another as desired, or in accordance with a given mathematical law. It follows that the machine need never be idle; for it can be set to tabulate successive values of any function, while the work of the tabulation can be suspended at any time to allow of the determination by it of one or more results of greater importance or urgency.
It can also ‘feel’ for particular events in the progress of its work—such, for instance, as a change of sign in the value of a function, or its approach to zero or infinity; and it can make any pre-arranged change in its procedure, when any such event occurs. Babbage dwells on these and similar points, and explains their bearing on the automatic solution (by approximation) of an equation of the th degree ;* but I have not been able to ascertain whether his way of attaining these results has or has not any resemblance to my method of so doing.
*C. Babbage: ‘Passages from the Life of a Philosopher’, p. 131.
The Analytical Machine is under the control of two keyboards, and in this respect differs from Babbage’s Engine. The upper key-board has ten keys (numbered 0 to 9), and is a means by which numbers are communicated to the machine. It can, therefore, undertake the work of the number-paper previously mentioned. The lower key-board can be used to control the working of the machine, in which case it performs the work of a formula-paper.
The key-boards are intended for use when the nature of the calculation does not warrant the preparation of a formula-paper or a number-paper, or when their use is not convenient. An interesting illustration of the use of the lower key-board is furnished by a case in which a person is desirous of solving a number of triangles (say) of which he knows the dimensions of the sides, but has not the requisite formula-paper for the purpose.
His best plan is to put a plain sheet of paper in the controlling apparatus, and on communicating to the machine the known dimensions of one of the triangles by means of the upper key-board, to guide the machine by means of the lower key-board to solve the triangle in accordance with the usual rule. The manipulations of the lower key-board will be recorded on the paper, which can then be used as a formula-paper to cause the machine automatically to solve the remaining triangles.
He can communicate to the machine the dimensions of these triangles individually by means of the upper key-board; or he may, if he prefers so doing, tabulate the dimensions in a number-paper, from which the machine will read them of its own accord. The machine is, therefore, able to ‘remember’, as it were, a mathematical rule; and having once been shown how to perform a certain calculation, it can perform any similar calculation automatically so long as the same paper remains in the machine.
It must be clearly understood that the machine is designed to be quite automatic in its action, so that a person almost entirely ignorant of mathematics could use it, in some respects, as successfully as the ablest mathematician. Suppose such a person desired to calculate the cosine of an angle, he obtains the correct result by inserting the formula-paper bearing the correct label, depressing the proper number-keys in succession to indicate the magnitude of the angle, and starting the machine, though he may be quite unaware of the definition, nature, or properties of a cosine.
While the machine is in use its central shaft must be maintained at an approximately uniform rate of rotation—a small motor might be used for this purpose. It is calculated that a velocity of three revolutions per second would be safe; and such a velocity would ensure the multiplication of any two Variables of twenty figures each in about 10 seconds, and their addition or subtraction in about three seconds. The time taken to divide one Variable by another depends on the degree of convergency of the series derived from the divisor, but l½ minutes may be taken as the probable maximum.
When constructing a formula-paper, due regard should therefore be had to the relatively long time required to accomplish the routine of division; and it will, no doubt, be found advisable to use this process as sparingly as possible. The determination of the logarithm of any number would take two minutes, while the evaluation of (for any value of ) by the exponential theorem, should not require more than l½ minutes longer—all results being of twenty figures.†
†The times given include that required for the selection of the Variables to be operated on.
The machine, as at present designed, would be about 26 inches long, 24 inches broad, and 20 inches high; and it would therefore be of a portable size. Of the exact dimensions of Babbage’s Engine I have no information; but evidently it was to have been a ponderous piece of machinery, measuring many feet in each direction.
The relatively large size of this engine is doubtless due partly to its being designed to accommodate the large number of one thousand Variables of fifty figures each, but more especially to the fact that the Variables were to have been stored on columns of wheels, which, while of considerable bulk in themselves, necessitated somewhat intricate gearing arrangements to control their movements. Again, Babbage’s method of multiplying by repeated additions, and of dividing by repeated subtractions, though from a mathematical point of view very simple, gave rise to very many mechanical complications. *
*See Report Brit. Assoc., 1878, p. 100.
To explain the power and scope of an Analytical Machine or Engine, I cannot do better than quote the words of the Countess of Lovelace: ‘There is no finite line of demarcation which limits the powers of the Analytical Engine. These powers are coextensive with the knowledge of the laws of analysis itself, and need be bounded only by our acquaintance with the latter.
Indeed, we may consider the engine as the material and mechanical representative of analysis, and that our actual working powers in this department of human study will be enabled more effectually than heretofore to keep pace with our theoretical knowledge of its principles and laws, through the complete control which the engine gives us over the executive manipulations of algebraical and numerical symbols.’†
†R. Taylor’s ‘Scientific Memoirs’, 1843, vol. iii., p. 696.
A Committee of the British Association which was appointed to report on Babbage’s Engine stated that, ‘apart from the question of its saving labor in operations now possible, we think the existence of such an instrument would place within reach much which, if not actually impossible, has been too close to the limits of human skill and endurance to be practically available’.‡
‡Report Brit. Assoc., 1878, p. 101.
In conclusion, I would observe that of the very numerous branches of pure and applied science which are dependent for their development, record, or application on the dominant science of mathematics, there is not one of which the progress would not be accelerated, and the pursuit would not be facilitated, by the complete command over the numerical interpretation of abstract mathematical expressions, and the relief from the time-consuming drudgery of computation, which the scientist would secure through the existence of machinery capable of performing the most tedious and complex calculations with expedition, automatism, and precision.
The image featured at the top of this post is ©G-Stock Studio/Shutterstock.com.






