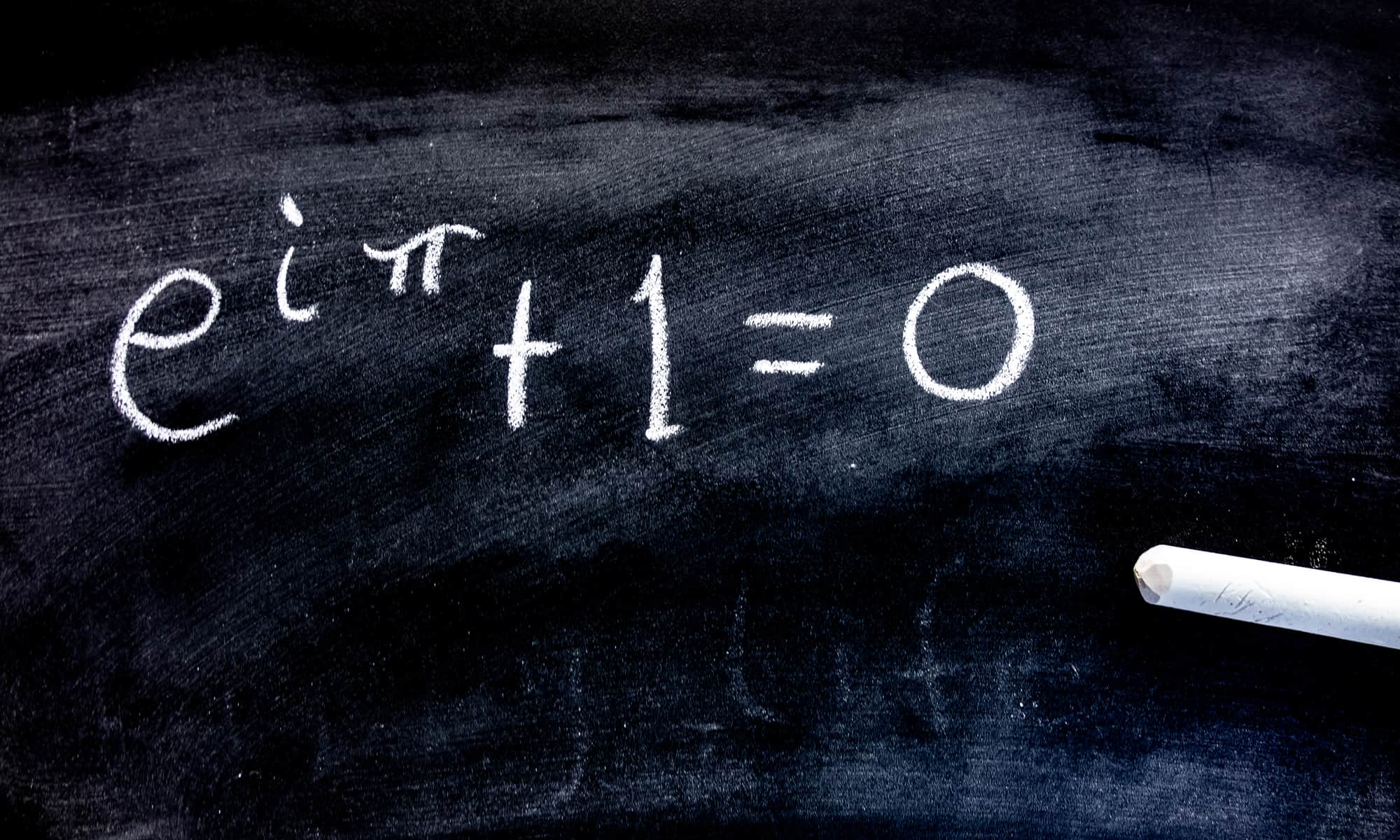What is Euler’s Identity, Earth’s ‘Most Beautiful Equation?’

Key Points:

• Richard Feynman, a physicist and Nobel Prize Winner, called Euler’s identity “our jewel” and regarded it as “the most remarkable formula in mathematics.” 
• The equation elegantly connects the five most critical mathematical identities across the fields of trigonometry, calculus, and complex numbers.
• Leonhard Euler, a Swiss mathematician born in the 18th century, created the Euler identity and other concepts like the Euler angle and the Euler Theorem that are still used in current mathematics.

Euler’s identity is often regarded as the “most beautiful mathematics equation” because of its simplicity and ability to show the relationship between five essential constants of mathematics. No other equation expresses the relationship of so many constants across various mathematical fields in such a simple way.

Euler’s identity helps us better understand complex numbers and their relationships with trigonometry. It has been beneficial in computer graphics, robotics, navigation, flight dynamics, orbital mechanics, and circuit analysis, where complex numbers and calculus are used.

Over the years, many great mathematicians and scientists have glorified this simple and elegant equation above other mathematical solutions. Richard Feynman, a physicist and Nobel Prize Winner, called it “our jewel” and regarded it as “the most remarkable formula in mathematics.” 

Although this equation is glorified by many, only a few understand it. To properly understand and appreciate Euler’s identity’s beauty, let’s explain the constants that make up the Euler identity.

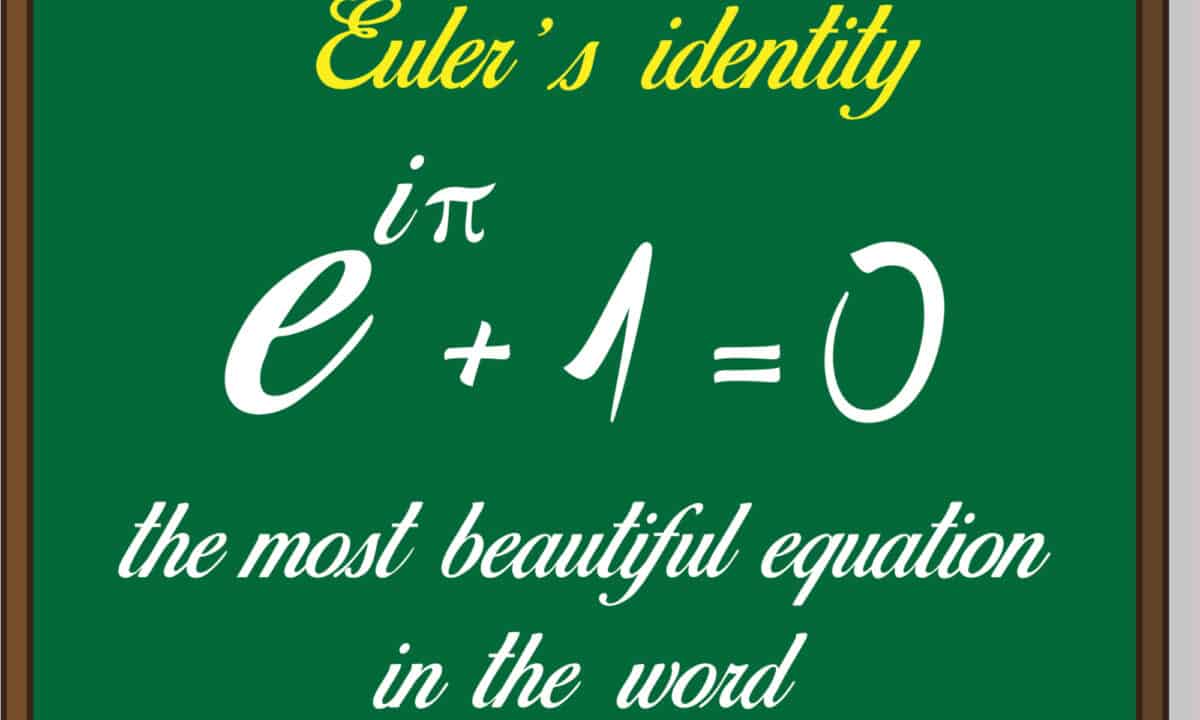
What is the Euler Identity?

Euler identity is often regarded as the most beautiful mathematics equation. The Euler identity is written as follows:

e^iπ + 1 = 0

The equation is considered beautiful because of its ability to represent profound and fundamental mathematical truth in a simple equation. This feat still amazes scientists and mathematicians around the world. The equation elegantly connects the five most critical mathematical identities across the fields of trigonometry, calculus, and complex numbers. The constants are:

• The addictive identity 0
• The pi constant
• The imaginary unit i
• The unit 1
• The base of a natural logarithm e

Euler Identity: Explanation of the Equations constants

To properly understand the Euler identity let’s take a step back to understand each of the constants in the Euler equation.

• The Euler’s number ‘e’: The Euler number is the base of the natural logarithm that is extensively used in calculus. It is a transcendental number with a value of 2.71828….
• The complex or imaginary unit(i): i is a complex number that had its value as the solution of the function ‘x²+1=0’ or simply the square root of -1 or t. It is commonly used in electrical and computer engineering for circuit analysis.
• The additive identity 0: ‘0’ is the first whole number in mathematics with an additive identity. Any number summed with zero equals the same number. 
• The pi ‘π’: The pi obtained by the ratio of a circle’s circumference to its diameter. It is the most popular and widely used mathematical constant.
• The unit ‘1’: It is the first natural number in mathematics and is very popular and valuable for its multiplicative identity — any number multiplied by this one is the same number.

Who created the Euler Identity?

Leonhard Euler, a Swiss mathematician born in the 18th century, created the Euler identity and other numerous concepts like the Euler angle and Euler Theorem still used in current mathematics. He spent most of his professional life in St. Petersburg, Russia. According to the United States Naval Academy (USNA), he is one of the most prolific mathematicians of all time. Euler wrote 886 articles and books. Much of his work was produced during the last two decades of his life when he was completely blind. Because he left so much work, the St. Petersburg Academy published it posthumously for more than 30 years.

Euler Identity: Practical Application in Real Life

Euler’s Identity results from interactions between complex numbers, which are numbers made up of two parts: An actual number and an imaginary number; for example, 6+9i. Complex numbers are used in various applications, including wave mechanics (a branch of physics) and the analysis of alternating current circuits in electrical engineering.

Furthermore, complex numbers and hyper complex numbers have a characteristic that makes them particularly helpful in computer graphics, robotics, navigation, flight dynamics, and orbital mechanics.

Euler Identity: Math Proof

Euler’s identity is a unique case of Euler’s formula, eiπ = cox + isinx, where x is equal to pi. When x is replaced with pi, 

e^iπ =cosπ + isinπ

we have the cosine of π to be equal to -1 and the sine of π to be equal to 0.

Therefore,  eⁱ = -1 + 0i. 

Which is equal to eⁱ = -1. 

Moving  the -1 on the left-hand side of the equation,

The result will be:

e^iπ + 1 = 0 which is our Euler identity

When using Euler’s Formula, don’t mistake degrees instead of radians when calculating the cosine and sine of x. Radians are another way to measure angles. So, in case you will be using a calculator, make sure your calculator is set to radians and not degrees.

Lastly, also know that mathematicians sometimes shorten cos x + i sin x as cis x. So, you may see the Euler formula written in this text or anywhere as: e^iπ = cis x

The image featured at the top of this post is ©FoxPix1/Shutterstock.com.